Sử dụng dữ liệu bài toán dưới đây để trả lời Bài 8, 9
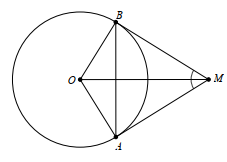
Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm)
Sử dụng dữ liệu bài toán dưới đây để trả lời Bài 8, 9
Cho đường tròn (O; R), lấy điểm M nằm ngoài (O) sao cho OM = 2R. Từ M kẻ tiếp tuyến MA và MB với (O) (A, B là các tiếp điểm)

Số đo góc \(\widehat {AOM}\) là
A. 30°.
B. 120°.
C. 50°.
D. 60°.
Câu hỏi trong đề: 12 bài tập Góc ở tâm và số đo cung bị chắn có lời giải !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Xét tam giác AOM vuông tại A ta có:
\(\cos AOM = \frac{{AO}}{{OM}} = \frac{R}{{2R}} = \frac{1}{2}\) suy ra \(\widehat {AOM} = 60^\circ \).
Câu hỏi cùng đoạn
Câu 2:
Số đo cung AB nhỏ là
A. 240°.
B. 120°.
C. 360°.
D. 210°.
Đáp án đúng là: B
Xét đường tròn (O) có MA, MB là hai tiếp tuyến cắt nhau tại M nên OM là tia phân giác của \(\widehat {AOB}\).
Suy ra \(\widehat {AOB} = 2\widehat {AOM} = 2.60^\circ = 120^\circ \) mà \(\widehat {AOB}\) là góc ở tâm chắn cung AB nên số đo cung nhỏ AB là 120°.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
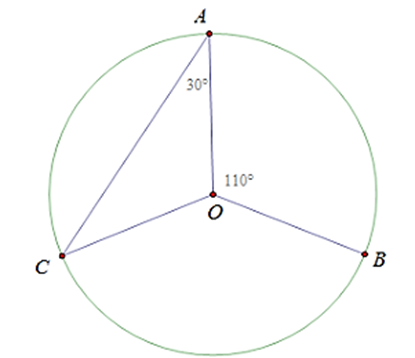
a) Ta có: (góc ở tâm chắn cung AB).
b) Xét tam giác AOB có AO = OB = R.
Suy ra tam giác AOB cân tại O nên \(\widehat {ACO} = \widehat {CAO} = 30^\circ \).
\(\widehat {AOC} + \widehat {ACO} + \widehat {CAO} = 180^\circ \) (tổng ba góc trong tam giác)
\(\widehat {AOC} + 30^\circ + 30^\circ = 180^\circ \)
Suy ra \(\widehat {AOC} = 180^\circ - \left( {30^\circ + 30^\circ } \right) = 120^\circ \).
Suy ra (góc ở tâm chắn cung AC).
c) Ta có: \(\widehat {BOC} + \widehat {AOC} + \widehat {AOB} = 360^\circ \).
Suy ra \(\widehat {BOC} = 130^\circ \).
Do đó số đo cung lớn BC bằng 130° .
Lời giải
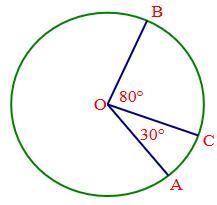
Điểm C nằm trên cung nhỏ AB nên ta có: sd (1)
Góc ở tâm \(\widehat {AOC} = 30^\circ \) chắn cung AC nên .
Góc ở tâm \(\widehat {BOC} = 80^\circ \) chắn cung BC nên .
Thay vào (1) ta được sd.
Câu 3
A. 240°.
B. 60°.
C. 180°.
D. 120°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 240°.
B. 60°.
C. 360°.
D. 210°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\widehat {AMO} = 35^\circ ,\widehat {MOB} = 55^\circ \).
B. \(\widehat {AMO} = 65^\circ ,\widehat {MOB} = 25^\circ \).
C. \(\widehat {AMO} = 25^\circ ,\widehat {MOB} = 65^\circ \).
D. \(\widehat {AMO} = 55^\circ ,\widehat {MOB} = 35^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.