15 câu trắc nghiệm Toán 9 Chân trời sáng tạo Bài 1. Hình trụ có đáp án
54 người thi tuần này 4.6 562 lượt thi 15 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Câu 1
A. \[r = 8{\rm{\;cm}};\,\,h = 6{\rm{\;cm}}.\]
B. \[r = 4{\rm{\;cm}};\,\,h = 3{\rm{\;cm}}.\]
C. \[r = 3{\rm{\;cm}};\,\,h = 4{\rm{\;cm}}.\]
D. \[r = 6{\rm{\;cm}};\,\,h = 8{\rm{\;cm}}.\]
Lời giải
Đáp án đúng là: D
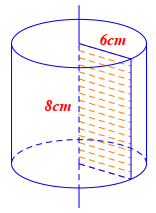
Ta có chiều cao của hình trụ là chiều dài của hình chữ nhật. Suy ra
\[h = 8{\rm{\;cm}}.\]
Lại có bán kính của hình trụ là chiều rộng của hình chữ nhật. Suy ra \[r = 6{\rm{\;cm}}.\]
Vậy ta chọn phương án D.
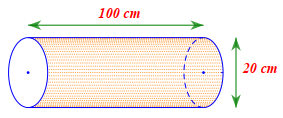
Câu 2
A. Chiều cao của hình trụ là \[20{\rm{\;cm}}\] và bán kính đáy là \[10{\rm{\;cm}}.\]
B. Chiều cao của hình trụ là \[50{\rm{\;cm}}\] và bán kính đáy là \[20{\rm{\;cm}}.\]
C. Chiều cao của hình trụ là \[100{\rm{\;cm}}\] và bán kính đáy là \[10{\rm{\;cm}}.\]
D. Chiều cao của hình trụ là \[100{\rm{\;cm}}\] và bán kính đáy là \[20{\rm{\;cm}}.\]
Lời giải
Đáp án đúng là: C
Quan sát hình vẽ, ta thấy:
⦁ Chiều cao của hình trụ bằng \[100{\rm{\;cm}}.\]
⦁ Đường kính đáy của hình trụ bằng \[20{\rm{\;cm}}.\]
Suy ra bán kính đáy của hình trụ bằng \[20:2 = 10\,\,\left( {{\rm{cm}}} \right).\]
Vậy ta chọn phương án C.
Câu 3
A. \[V = \frac{4}{3}\pi {r^2}h.\]
B. \[V = \frac{2}{3}\pi {r^2}h.\]
C. \[V = \pi {r^2}h.\]
D. \[V = \frac{1}{3}\pi {r^2}h.\]
Lời giải
Đáp án đúng là: C
Thể tích \[V\] của hình trụ \[\left( T \right)\] có công thức là: \[V = \pi {r^2}h.\]
Do đó ta chọn phương án C.
Câu 4
A. \[{S_{xq}} = 2\pi rl.\]
B. \[{S_{xq}} = \pi rl.\]
C. \[{S_{xq}} = \pi {r^2}h.\]
D. \[{S_{xq}} = \pi rh.\]
Lời giải
Đáp án đúng là: A
Ta có chiều cao của hình trụ bằng độ dài đường sinh của hình trụ. Suy ra \[h = l.\]
Diện tích xung quanh \[{S_{xq}}\] của hình trụ \[\left( T \right)\] có công thức là: \[{S_{xq}} = 2\pi rh = 2\pi rl.\]
Do đó ta chọn phương án A.
Câu 5
A. \[{S_{tp}} = \pi rl + \pi {r^2}.\]
B. \[{S_{tp}} = 2\pi rh + 2\pi {r^2}.\]
C. \[{S_{tp}} = \pi rh + \pi {r^2}.\]
D. \[{S_{tp}} = \pi rl + 2\pi {r^2}.\]
Lời giải
Đáp án đúng là: B
Diện tích toàn phần \[{S_{tp}}\] của hình trụ \[\left( T \right)\] có công thức là: \[{S_{tp}} = 2\pi rh + 2\pi {r^2}.\]
Do đó ta chọn phương án B.
Câu 6
A. \[14\pi {\rm{\;d}}{{\rm{m}}^3}.\]
B. \[56\pi {\rm{\;d}}{{\rm{m}}^3}.\]
C. \[28\pi {\rm{\;d}}{{\rm{m}}^3}.\]
D. \[7\pi {\rm{\;d}}{{\rm{m}}^3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[6\pi {\rm{\;c}}{{\rm{m}}^2}.\]
B. \[12{\rm{\;c}}{{\rm{m}}^2}.\]
C. \[12\pi {\rm{\;c}}{{\rm{m}}^2}.\]
D. \[18\pi {\rm{\;c}}{{\rm{m}}^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \[2\,\,813,44{\rm{\;c}}{{\rm{m}}^2}.\]
B. \[1\,\,055,04{\rm{\;c}}{{\rm{m}}^2}.\]
C. \[2\,\,110,08{\rm{\;c}}{{\rm{m}}^2}.\]
D. \[1\,\,205,76{\rm{\;c}}{{\rm{m}}^2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[700\pi {\rm{\;c}}{{\rm{m}}^3}.\]
B. \[490\pi {\rm{\;c}}{{\rm{m}}^3}.\]
C. \[980\pi {\rm{\;c}}{{\rm{m}}^3}.\]
D. \[\frac{{490\pi }}{3}{\rm{\;c}}{{\rm{m}}^3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[27,25{\rm{\;cm}}.\]
B. \[32,25{\rm{\;cm}}.\]
C. \[70,5{\rm{\;cm}}.\]
D. \[{\rm{54,5\;cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[\frac{8}{3}{\rm{\;cm}}.\]
B. \[\frac{{4\sqrt 3 \pi }}{3}{\rm{\;cm}}.\]
C. \[\frac{{4\pi }}{3}{\rm{\;cm}}.\]
D. \[\frac{{8\pi }}{3}{\rm{\;cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. gấp 4 lần thể tích cũ.
B. gấp 8 lần thể tích cũ.
C. gấp 12 lần thể tích cũ.
D. gấp 16 lần thể tích cũ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \[96\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
B. \[110\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
C. \[112\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
D. \[128\pi {\rm{\;(c}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \[\frac{\pi }{2}.\]
B. \[\frac{\pi }{4}.\]
C. \[\frac{\pi }{{12}}.\]
D. \[\frac{{2\pi }}{3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \[V = 16\pi {a^3}.\]
B. \[V = 8\pi {a^3}.\]
C. \[V = 4\pi {a^3}.\]
D. \[V = 12\pi {a^3}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.