12 bài tập Chứng minh đẳng thức liên quan đến tỉ số lượng giác có lời giải
51 người thi tuần này 4.6 184 lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
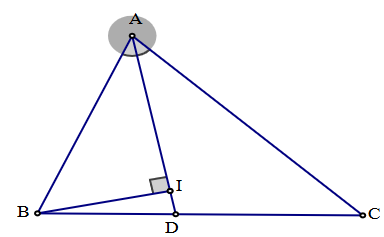
Vẽ đường phân giác AD của tam giác ABC.
Theo tính chất đường phân giác của tam giác, ta có: \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
Suy ra \(\frac{{BD}}{{AB}} = \frac{{BD + DC}}{{AB + AC}} = \frac{{BC}}{{AC + AC}}\).
Vậy \(\frac{{BD}}{{AB}} = \frac{a}{{b + c}}\).
Kẻ BI⊥AD (I ∈ AD), suy ra BI ≤ BD.
∆IAB có \(\widehat {AIB} = 90^\circ \).
Do đó, sin\(\widehat {BAI}\) = \(\frac{{BI}}{{AB}}\) hay \(\sin \frac{A}{2} \le \frac{a}{{b + c}}\).
Lời giải
Hướng dẫn giải
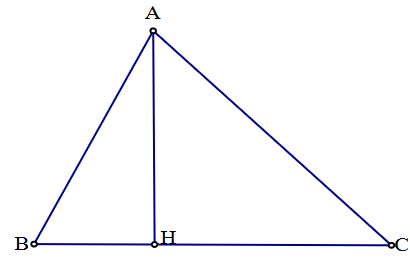
Vẽ AH⊥BC, H ∈ BC.
Vì trong tam giác HAB có \(\widehat H = 90^\circ \) nên sin B = \(\frac{{AH}}{{AB}}\).
Do trong tam giác AHC có \(\widehat H = 90^\circ \) nên sin C = \(\frac{{AH}}{{AC}}\).
Do đó, \(\frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{AB}} = \frac{b}{c}\) suy ra \(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\).
Tương tự, ta suy ra \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}}\).
Vậy \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\).
Lời giải
Hướng dẫn giải
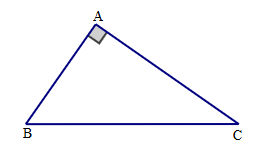
Xét tam giác ABC vuông tại A, ta có:
sinB = \(\frac{{AC}}{{BC}}\); sinC = \(\frac{{AB}}{{BC}}\).
Do đó, \(\frac{{\sin B}}{{\sin C}} = \frac{{AC}}{{BC}}:\frac{{AB}}{{BC}} = \frac{{AC}}{{BA}}\) (đpcm).
Câu 4
A. \({\cos ^2}\frac{\alpha }{2} + {\sin ^2}\frac{\alpha }{2} = \frac{1}{2}\).
B. \({\cos ^2}\frac{\alpha }{3} + {\sin ^2}\frac{\alpha }{3} = \frac{1}{3}\).
C. \({\cos ^2}\frac{\alpha }{4} + {\sin ^2}\frac{\alpha }{4} = \frac{1}{4}\).
D. \(5\left( {{{\cos }^2}\frac{\alpha }{5} + {{\sin }^2}\frac{\alpha }{5}} \right) = 5\).
Lời giải
Đáp án đúng là: D
Ta có: cos2α + sin2α = 1 với 0° ≤ α ≤ 180° nên ta cũng có:
\({\cos ^2}\frac{\alpha }{5} + {\sin ^2}\frac{\alpha }{5}\) = 1.
Suy ra \(5\left( {{{\cos }^2}\frac{\alpha }{5} + {{\sin }^2}\frac{\alpha }{5}} \right) = 5\).
Câu 5
A. sinA = sin(B + C).
B. tanA = tan(B + C).
C. cos\(\frac{A}{2}\) = sin\(\frac{{B + C}}{2}\) .
D. tanA = −tan(B + C).
Lời giải
Đáp án đúng là: B
Xét tam giác ABC, ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) nên \(\widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right)\)
hay \(\widehat B + \widehat C = 180^\circ - \widehat A\).
Do đó sin A = sin (180° − \(\widehat A\)) = sin (B + C).
Suy ra khẳng định A là đúng.
Lại có \(\widehat A + \widehat B + \widehat C = 180^\circ \) suy ra \(\frac{{\widehat A + \widehat B + \widehat C}}{2} = \frac{{180^\circ }}{2} = 90^\circ \).
Do đó: cos\(\frac{A}{2}\) = sin\(\frac{{B + C}}{2}\) (hai góc phụ nhau).
Suy ra khẳng định C là đúng.
Mặt khác tanA = −tan(180° − A) = −tan(B + C).
Suy ra khẳng định D là đúng.
Vậy chọn đáp án B.
Câu 6
A. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x + 1}}{{\tan x - 1}}\).
B. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x}}{{\tan x - 1}}\).
C. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{\tan x + 1}}{{\tan x}}\).
D. \(\frac{{1 + \cot x}}{{1 - \cot x}} = \frac{{{{\tan }^2}x + 1}}{{\tan x - 1}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 1.
B. 1 + 2sinxcosx.
C. 1 – 2sinxcosx.
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. sin4x + cos4x = 1.
B. sin4x + cos4x = sin2x – cos2x.
C. sin4x + cos4x = 1 – 2sin2xcos2x.
D. sin4x + cos4x = 1 + 2sin2xcos2x.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 0.
B. 2 – 2sin2xcos2x.
C. 2 + 4sin2xcos2x.
D. 2 – 4sin2xcos2x.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 3sin2xcos2x.
B. sin2x.
C. 1 – 3sin2xcos2x.
D. 2 + sin2x.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.