12 bài tập Tính bán kính đường tròn có lời giải
28 người thi tuần này 4.6 173 lượt thi 12 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Câu 1
A. R = \(3\sqrt 2 \) cm.
B. R = \(\frac{{3\sqrt 2 }}{2}\) cm.
C. R = 3 cm.
D. R = \(\frac{{3\sqrt 3 }}{2}\) cm.
Lời giải
Đáp án đúng là: B
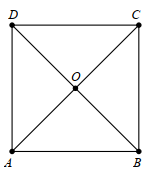
Gọi O là giao hai đường chéo của hình vuông ABCD. Khi đó theo tính chất của hình vuông, ta có: OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = \(\frac{{AC}}{2}\).
Xét tam giác ABC vuông cân tại B, ta có:
AC = \(\sqrt {A{B^2} + B{C^2}} = 3\sqrt 2 \)
Suy ra OA = \(\frac{{AC}}{2} = \frac{{3\sqrt 2 }}{2}\).
Vậy bán kính của đường tròn là R = OA = \(\frac{{3\sqrt 2 }}{2}\) cm.
Câu 2
A. R = 25.
B. R = \(\frac{{25}}{2}\).
C. R = 15.
D. R = 20.
Lời giải
Đáp án đúng là: B

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền BC, ban kính R = \(\frac{{BC}}{2}\).
Theo định lí Pythagore ta có: BC = \(\sqrt {A{C^2} + A{B^2}} = 25\) nên bán kính R = \(\frac{{25}}{2}\).
Câu 3
A. R = 26.
B. R = 13.
C. R = \(\frac{{13}}{2}\).
D. R = 6.
Lời giải
Đáp án đúng là: C

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm của cạnh huyền BC, ban kính R = \(\frac{{BC}}{2}\).
Theo định lí Pythagore ta có: BC = \(\sqrt {A{C^2} + A{B^2}} = 13\) nên bán kính R = \(\frac{{13}}{2}\).
Câu 4
A. R = 7,5 cm.
B. R = 13 cm.
C. R = 6 cm.
D. R = 6,5 cm.
Lời giải
Đáp án đúng là: D
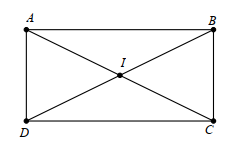
Gọi I là giao điểm của hai đường chéo, ta có: IA = IB = IC = ID (vì BD = AC và I là trung điểm của mỗi đường).
Nên bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính R = \(\frac{{AC}}{2}\).
Theo định lí Pythagore trong tam giác ABC ta có:
AC = \(\sqrt {B{C^2} + A{B^2}} = 13\) cm.
Do đó, R = \(\frac{{AC}}{2}\) = 6,5 cm.
Vậy bán kính cần tìm là R = 6,5 cm.
Câu 5
Cho hình chữ nhật ABCD có AB = 8 cm, BC = 6 cm. Tính bán kính đường tròn đi qua bốn đỉnh A, B, C, D.
A. R = 5 cm.
B. R = 10 cm.
C. R = 6 cm.
D. R = 2,5 cm.
Lời giải
Đáp án đúng là: A
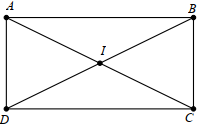
Gọi I là giao điểm của hai đường chéo, ta có: IA = IB = IC = ID (vì DB = AC và I là trung điểm mỗi đường)
Nên bốn điểm A, B, C, D cùng thuộc đường tròn tâm I bán kính R = \(\frac{{AC}}{2}\).
Theo định lí Pythagore trong tam giác vuông ABC, ta có:
AC = \(\sqrt {B{C^2} + A{B^2}} = \sqrt {{6^2} + {8^2}} = 10\) nên R = \(\frac{{AC}}{2}\) = 5 cm.
Vậy bán kính cần tìm là R = 5 cm.
Câu 6
A. \(\sqrt 3 \)cm.
B. \(\sqrt 5 \) cm.
C. \(\frac{{\sqrt 5 }}{2}\) cm.
D. \(\frac{{\sqrt 3 }}{2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 2 cm.
B. 4 cm.
C. 6 cm.
D. 8 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. R = 5 cm.
B. R = 10 cm.
C. R = \(2\sqrt 5 \) cm.
D. R = \(\sqrt 5 \) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. d = 8 cm.
B. d = 12 cm.
C. d = 10 cm..
D. d = 5 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 24 cm2.
B. \(24\sqrt 3 \) cm2.
C. 12 cm2.
D. \(12\sqrt 3 \) cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.