Cho tam giác ABC có BC = a, AC = b, AB = c. Chứng minh rằng \(\sin \frac{A}{2} \le \frac{a}{{b + c}}\).
Quảng cáo
Trả lời:
Hướng dẫn giải
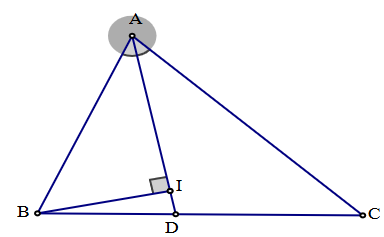
Vẽ đường phân giác AD của tam giác ABC.
Theo tính chất đường phân giác của tam giác, ta có: \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
Suy ra \(\frac{{BD}}{{AB}} = \frac{{BD + DC}}{{AB + AC}} = \frac{{BC}}{{AC + AC}}\).
Vậy \(\frac{{BD}}{{AB}} = \frac{a}{{b + c}}\).
Kẻ BI⊥AD (I ∈ AD), suy ra BI ≤ BD.
∆IAB có \(\widehat {AIB} = 90^\circ \).
Do đó, sin\(\widehat {BAI}\) = \(\frac{{BI}}{{AB}}\) hay \(\sin \frac{A}{2} \le \frac{a}{{b + c}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
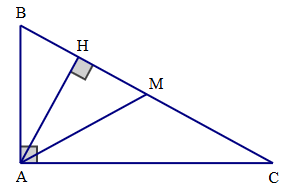
a) Ta có: \(\widehat {AMH} = 2\alpha \).
Suy ra sin2α = \(\frac{{AH}}{{AM}} = \frac{{2AH}}{{2AM}} = \frac{{2AH}}{{BC}} = 2\frac{{AB.AC}}{{B{C^2}}} = 2\sin \alpha .\cos \alpha \).
b) 1 + cos2α = \(1 + \sin \widehat {AMH} = 1 + \frac{{HM}}{{AM}} = \frac{{HC}}{{AM}} = \frac{{2HC}}{{BC}} = 2.\frac{{A{C^2}}}{{B{C^2}}} = 2{\cos ^2}\alpha \).
c) 1 – cos2α = \(1 - \cos \widehat {AMH} = 1 - \frac{{HM}}{{AM}} = \frac{{HB}}{{AM}} = \frac{{2BH}}{{BC}} = 2.\frac{{A{B^2}}}{{B{C^2}}} = 2{\sin ^2}\alpha \).
Lời giải
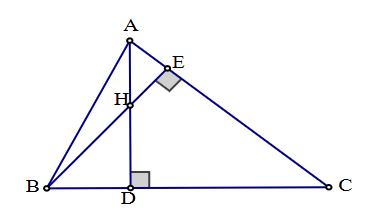
Ta có: tanB = \(\frac{{AD}}{{BD}}\); tanC = \(\frac{{AD}}{{CD}}\) suy ra tanB.tanC = \(\frac{{A{D^2}}}{{CD.BD}}\) (1)
Có \(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)); \(\widehat {HDB} = \widehat {ADC}\) = 90°.
Do đó, ∆BDH và ∆ADC đồng dạng theo trường hợp góc góc.
Suy ra \(\frac{{DH}}{{DC}} = \frac{{BD}}{{AD}}\), do đó BD.DC = DH.AD (2).
Từ (1) và (2) suy ra tanB.tanC = \(\frac{{A{D^2}}}{{DH.AD}} = \frac{{AD}}{{DH}}\) (3).
Theo giả thiết \(\frac{{HD}}{{AH}} = \frac{1}{2}\) suy ra \(\frac{{HD}}{{AH + HD}} = \frac{1}{3}\) hay \(\frac{{HD}}{{AD}} = \frac{1}{3}\).
Suy ra AD = 3HD.
Thay vào (3), ta được: tanB.tanC = \(\frac{{3HD}}{{HD}}\) = 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 3sin2xcos2x.
B. sin2x.
C. 1 – 3sin2xcos2x.
D. 2 + sin2x.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. sinA = sin(B + C).
B. tanA = tan(B + C).
C. cos\(\frac{A}{2}\) = sin\(\frac{{B + C}}{2}\) .
D. tanA = −tan(B + C).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.