khoahoc.vietjack.com
Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Lớp 9
  3. Toán

Câu hỏi:

02/10/2024 295 Lưu

Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9\end{array} \right.?\) 

A. \(\left( {1;\,\,1} \right).\) 
B. \(\left( {1;\,\, - 1} \right).\) 
C. \(\left( { - 21;\,\,15} \right).\) 
D. \(\left( {21;\,\, - 15} \right).\)
Xem lời giải

Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Đáp án đúng là: C

Cách 1. Sử dụng MTCT để tìm nghiệm của hệ hai phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)

Với MTCT phù hợp, ta bấm lần lượt các phím:

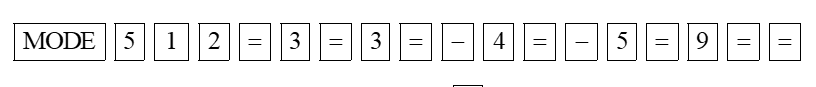
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9\end{array} \right.?\) A. \(\left( {1;\,\,1} \right).\) B. \(\left( {1;\,\, - 1} \right).\) C. \(\left( { - 21;\,\,15} \right).\) D. \(\left( {21;\,\, - 15} \right).\) (ảnh 1) 

Trên màn hình cho kết quả \(x = - 21,\) ta bấm tiếp phím  màn hình cho kết quả \(y = 15.\)

Vậy cặp số \(\left( { - 21;\,\,15} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)

Cách 2. Thay \(x = 1;\,\,y = 1\) vào hệ phương trình đã cho, ta được: \(\left\{ \begin{array}{l}2 \cdot 1 + 3 \cdot 1 = 5\,\,\left( { \ne 3} \right)\\ - 4 \cdot 1 - 5 \cdot 1 = - 9\,\,\left( { \ne 9} \right)\end{array} \right..\)

Tương tự, thay giá trị của \(x\) và \(y\) lần lượt của các cặp số ở phương án B, C, D vào hệ phương trình đã cho, ta thấy chỉ có cặp số \(\left( { - 21;\,\,15} \right)\) là nghiệm của cả hai phương trình trong hệ.

Vậy cặp số \(\left( { - 21;\,\,15} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)

Cách 3. Giải hệ phương trình \(\left\{ \begin{array}{l}2x + 3y = 3\\ - 4x - 5y = 9.\end{array} \right.\)

Nhân hai vế của phương trình thứ nhất với \(2,\) ta được hệ phương trình mới \(\left\{ \begin{array}{l}4x + 6y = 6\\ - 4x - 5y = 9.\end{array} \right.\)

Cộng từng vế hai phương trình của hệ phương trình trên, ta được: \(y = 15.\)

Thay \(y = 15\) vào phương trình \(2x + 3y = 3,\) ta được:

\(2x + 3 \cdot 15 = 3,\) hay \(2x + 45 = 3,\) suy ra \(2x = - 42,\) nên \(x = - 21.\)

Vậy hệ phương trình đã cho có nghiệm duy nhất là \(\left( { - 21;\,\,15} \right).\)

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:
  1. Combo 3 khóa học Toán - Văn - Anh lớp 1-12 chỉ với 250k
  2. Phòng luyện 1000 đề VIP Đgnl các trường ĐHQGHN, Tp.HCM, Bách Khoa, tốt nghiệp THPT chỉ với 399k
  3. Mã giảm giá 20% sản phẩm sách VietJack trên Shopee mall
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác \(ABC\) vuông tại \(A\). Khi đó, \(\sin \widehat {ABC}\) bằng: 
A. \(\frac{{AC}}{{BC}}.\)
B. \(\frac{{BC}}{{AC}}.\)
C. \(\frac{{AB}}{{BC}}.\) 
D. \(\frac{{AB}}{{AC}}.\)

Lời giải

Đáp án đúng là: A

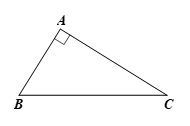
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó, \(\sin \widehat {ABC}\) bằng: A. \(\frac{{AC}}{{BC}}.\) B. \(\frac{{BC}}{{AC}}.\) C. \(\frac{{AB}}{{BC}}.\) D. \(\frac{{AB}}{{AC}}.\) (ảnh 1)

Tam giác \[ABC\] vuông tại \[A\], ta có: \[\sin \widehat {ABC} = \frac{{AC}}{{BC}}\].

Vậy ta chọn phương án A.
 

Câu 2

Cho \(\alpha \) và \(\beta \) là hai góc nhọn bất kì thỏa mãn \(\alpha + \beta = 90^\circ .\) Khẳng định nào sau đây là đúng? 
A. \(\tan \alpha = \sin \beta .\) 
B. \(\tan \alpha = \cot \beta .\) 
C. \(\tan \alpha = \cos \beta .\) 
D. \(\tan \alpha = \tan \beta .\)

Lời giải

Đáp án đúng là: B

Với \(\alpha + \beta = 90^o ,\) ta có: \(\sin \alpha = \cos \beta ;\,\,\cos \alpha = \sin \beta ;\,\,\tan \alpha = \cot \beta ;\,\,\cot \alpha = \tan \beta .\)

Vậy ta chọn phương án B.

Câu 3

Giải bất phương trình ẩn \[x\] sau: \[\frac{{x - ab}}{{a + b}} + \frac{{x - bc}}{{b + c}} + \frac{{x - ac}}{{a + c}} > a + b + c\] với \[a,\,\,b,\,\,c > 0\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Điều kiện xác định của phương trình \(\frac{1}{{x\left( {{x^2} + 4} \right)}} = \frac{{x + 1}}{x} - \frac{1}{{x - 2}}\) là 
A. \(x \ne 0,\,\,\;x\; \ne \; - 2\) và \(x \ne 2.\) 
B. \(x \ne 0\) và \(x \ne - 2.\) 
C. \(x \ne 0\) và \(x \ne - 4.\)
D. \(x \ne 0\) và \(x \ne 2.\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Từ một đài quan sát, một người đặt mắt tại vị trí \[B.\] Người đó nhìn thấy một chiếc ô tô ở vị trí \[C\] theo phương \[BC\] tạo với phương nằm ngang \[Bx\] một góc là \(\widehat {CBx} = 25^\circ \) với \[Bx\,{\rm{//}}\,AC.\] Khi đó, khoảng cách giữa ô tô và chân đài quan sát là \[AC = 1,221{\rm{\;km}}{\rm{.}}\] Nếu ô tô từ vị trí \[C\] tiếp tục đi về phía chân đài quan sát với tốc độ \[60\] km/h thì sau 1 phút, người đó nhìn thấy ô tô ở vị trí \[D\] với góc \(\widehat {DBx} = \alpha \) (hình vẽ).
Từ một đài quan sát, một người đặt mắt tại vị trí B Người đó nhìn thấy một chiếc ô tô ở vị trí C theo phương BC tạo với phương nằm ngang Bx một góc là (ảnh 1)

a) Tính chiều cao của đài quan sát (làm tròn kết quả đến hàng đơn vị của mét), biết độ cao từ tầm mắt của người đó đến đỉnh đài quan sát là \[3\] m.

b) Tính số đo góc \[\alpha \] (làm tròn kết quả đến hàng đơn vị của phút).

c) Tính khoảng cách từ mắt người quan sát đến vị trí \[D\] (làm tròn kết quả đến hàng đơn vị của mét).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

1. Giải các phương trình sau:

a) \(\left( {1 - 2x} \right)\left( {x + 5} \right) = 0.\)     b) \(\frac{{x + 2}}{{x - 2}} - \frac{{x - 2}}{{2 + x}} = \frac{{{x^2} + 16}}{{{x^2} - 4}}.\)

2. Giải các bất phương trình sau:

a) \(3x - 8 > 4x - 12.\)   b) \(\frac{{2 - x}}{4} < 5\).       c) \[{\left( {x - 4} \right)^2} - \left( {x + 5} \right)\left( {x - 5} \right) \ge  - 8x + 41.\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho tam giác \(MNP\) vuông tại \(M\) có \(MP = 4\) và \(\widehat {P\,} = 30^o .\) Nhận định nào sau đây là sai? 
A. \(MN = \frac{{4\sqrt 3 }}{3}\). 
B. \(NP = 8\). 
C. \(\widehat {N\,} = 60^o .\) 
D. \(\tan P \cdot \cot P = 1\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của VietJack.

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập