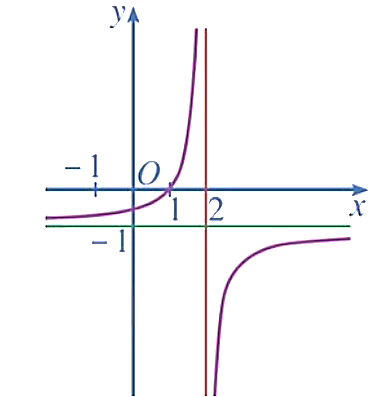
Cho hàm số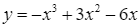 
. Khẳng định nào sau đây là đúng?
. Khẳng định nào sau đây là đúng?A. Hàm số đã cho đồng biến trên khoảng 
B. Hàm số đã cho nghịch biến trên khoảng 
.
C. Hàm số đã cho có một cực trị.
D. Hàm số đã cho có hai cực trị.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
TXĐ của hàm số là \(\mathbb{R}\).
Ta có: \(y' = - 3{x^2} + 6x - 6 = - 3\left( {{x^2} - 2x + 1} \right) - 3 = - 3{\left( {x - 1} \right)^2} - 3 < 0\,\,\forall x \in \mathbb{R}\).
Vậy hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\) và hàm số không có cực trị.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
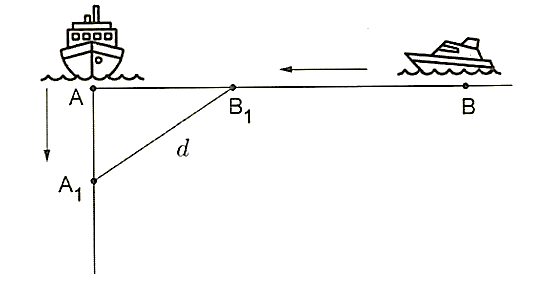
Tại thời điểm 
(giờ) sau khi xuất phát, khoảng cách giữa hai tàu là 
. Khi đó, tàu 
đang ở vị trí 
và tàu 
đang ở vị trí 
như hình vẽ trên.
Ta có: 
.
Suy ra 
.
Xét hàm số 
với 
.
Ta có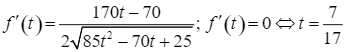 
.
Bảng biến thiên của hàm số 
trên khoảng 
như sau:
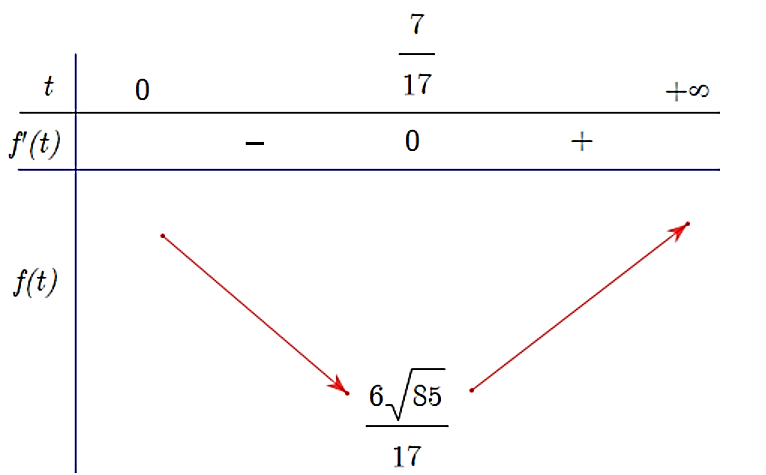
Từ bảng biến thiên, ta có: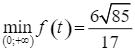 
tại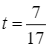 
.
Vậy sau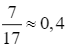 
giờ thì khoảng cách giữa hai tàu là bé nhất.
Đáp số: 
.
Lời giải
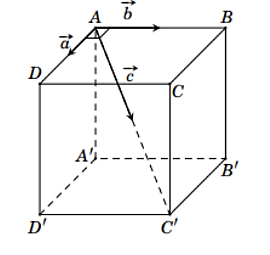
Từ giả thiết, ta suy ra được:
; 
.
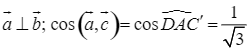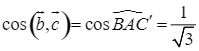Giả sử lực tổng hợp là 
, tức là 
.
Khi đó, 
.
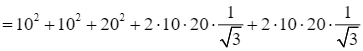
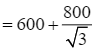Suy ra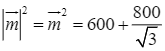 
. Do đó, 
.
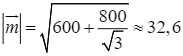Vậy độ lớn hợp lực của các lực 
bằng khoảng 
N.
Đáp số: .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 
; 
.
; . B. 
; 
.
; .C. 
; 
.
; .D. 
; 
.
; .Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo