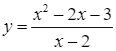Cho hàm số 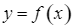 xác định trên
xác định trên 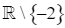 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
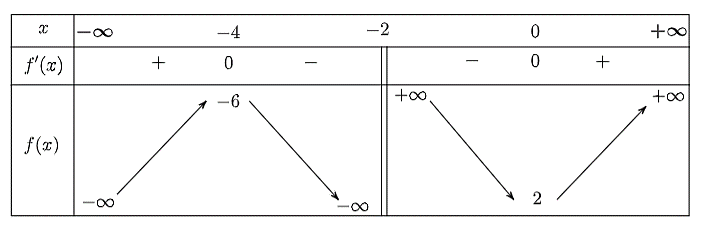
a) Hàm số 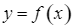 đồng biến trên mỗi khoảng
đồng biến trên mỗi khoảng 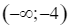 và
và 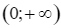 .
.
b) Giá trị cực tiểu của hàm số đã cho là 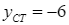 .
.
c) Hàm số 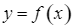 có giá trị lớn nhất bằng
có giá trị lớn nhất bằng 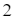 và giá trị nhỏ nhất bằng
và giá trị nhỏ nhất bằng 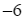 .
.
d) Công thức xác định hàm số là 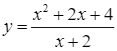 .
.
Cho hàm số ![]() xác định trên
xác định trên ![]() và có bảng biến thiên như sau:
và có bảng biến thiên như sau:

a) Hàm số ![]() đồng biến trên mỗi khoảng
đồng biến trên mỗi khoảng ![]() và
và ![]() .
.
b) Giá trị cực tiểu của hàm số đã cho là ![]() .
.
c) Hàm số ![]() có giá trị lớn nhất bằng
có giá trị lớn nhất bằng ![]() và giá trị nhỏ nhất bằng
và giá trị nhỏ nhất bằng ![]() .
.
d) Công thức xác định hàm số là 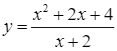 .
.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
a) Đ, b) S, c) S, d) Đ.
Hướng dẫn giải
– Từ bảng biến thiên, ta thấy ![]() với mọi
với mọi ![]() , do đó hàm số
, do đó hàm số ![]() đồng biến trên mỗi khoảng
đồng biến trên mỗi khoảng ![]() và
và ![]() , vậy ý a) đúng.
, vậy ý a) đúng.
– Hàm số đạt cực đại tại ![]() ,
, ![]() ; hàm số đạt cực tiểu tại
; hàm số đạt cực tiểu tại ![]() ,
, ![]() , do đó ý b) sai.
, do đó ý b) sai.
– Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên ![]() nên ý c) sai.
nên ý c) sai.
– Xét hàm số 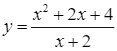 , ta có:
, ta có:
+ Tập xác định của hàm số là ![]() .
.
+ Có 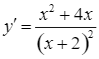 ;
; ![]() khi
khi ![]() hoặc
hoặc ![]() .
.
+ Trên các khoảng ![]() và
và ![]() ,
, ![]() .
.
Trên các khoảng ![]() và
và ![]() ,
, ![]() .
.
+ Hàm số đạt cực đại tại ![]() ,
, ![]() ; hàm số đạt cực tiểu tại
; hàm số đạt cực tiểu tại ![]() ,
, ![]() .
.
+ Đường thẳng ![]() là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Vậy bảng biến thiên đã cho là bảng biến thiên của hàm số 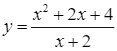 nên ý d) đúng.
nên ý d) đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
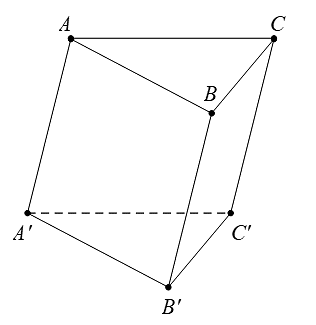
Vì ![]() là hình lăng trụ nên
là hình lăng trụ nên ![]() .
.
Do đó, ![]() .
.
Mà tam giác ![]() đều nên
đều nên ![]() . Vậy
. Vậy ![]() .
.
Lời giải
Do hàm số ![]() xác định trên
xác định trên ![]() nên hàm số
nên hàm số ![]() cũng xác định trên
cũng xác định trên ![]() .
.
Ta có ![]() ;
; ![]() khi
khi ![]() .
.
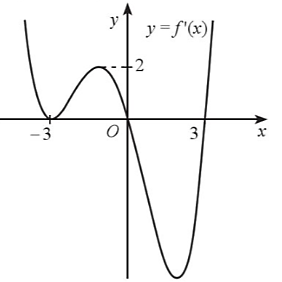
Số nghiệm của phương trình ![]() là số giao điểm của đồ thị hàm số
là số giao điểm của đồ thị hàm số ![]() và đường thẳng
và đường thẳng ![]() .
.
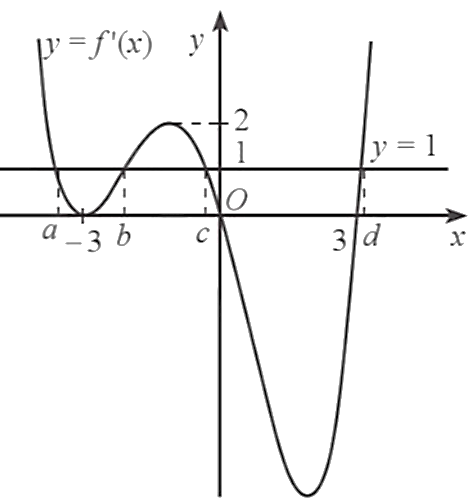
Căn cứ vào đồ thị hàm số, ta thấy phương trình ![]() hay
hay ![]() có 4 nghiệm phân biệt. Gọi 4 nghiệm đó theo thứ tự từ bé đến lớn là
có 4 nghiệm phân biệt. Gọi 4 nghiệm đó theo thứ tự từ bé đến lớn là ![]() .
.
Dựa vào vị trí của đồ thị hàm số ![]() và đường thẳng
và đường thẳng ![]() , ta có bảng xét dấu
, ta có bảng xét dấu ![]() như sau:
như sau:

Vậy hàm số ![]() có 4 điểm cực trị.
có 4 điểm cực trị.
Đáp số: 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.