Câu hỏi:

09/10/2024 2,937

Tiệm cận xiên của đồ thị hàm số \(y = \frac{{{x^2} - 3x + 6}}{{x + 2}}\) là đường thẳng:

A. \(y = x - 5\).

B. \(y = x + 5\).

C. \(y = x + 2\).

D. \(y = x - 3\).

Xem lời giải

Câu hỏi trong đề: Đề thi giữa kì 1 Toán 12 Kết Nối Tri Thức có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án đúng là: A

Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).

Ta có: \(y = \frac{{{x^2} - 3x + 6}}{{x + 2}} = x - 5 + \frac{{16}}{{x + 2}}\).

\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x - 5} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{16}}{{x + 2}} = 0\); \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x - 5} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{{16}}{{x + 2}} = 0\).

Vậy đường thẳng \(y = x - 5\) là tiệm cận xiên của đồ thị hàm số đã cho.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\).

a) Hàm số đã cho đồng biến trên \[\left( { - \infty ; - 1} \right)\] và \(\left( {3; + \infty } \right)\).

b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \( - 4\).

c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\).

d) Phương trình tiếp tuyến của đồ thị hàm số đã cho vuông góc với đường thẳng \(x - 3y - 6 = 0\) đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).

Xem đáp án

Lời giải

a) S, b) S, c) Đ, d) Đ.

Hướng dẫn giải

Xét hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}} = x + 1 + \frac{1}{{x + 2}}\).

– Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ { - 2} \right\}\).

– Ta có \(y' = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\); \(y' = 0\) khi \(x = - 3\) hoặc \(x = - 1\).

Bảng biến thiên của hàm số như sau:

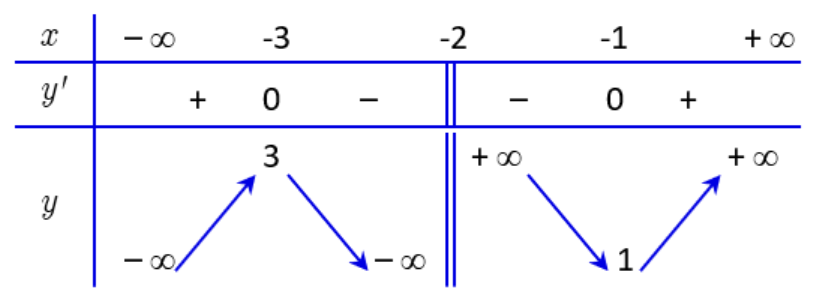
– Hàm số đã cho đồng biến trên từng khoảng \(\left( { - \infty ; - 3} \right)\) và \(\left( { - 1; + \infty } \right)\). Do đó, ý a) sai.

– Hàm số đã cho đạt cực đại tại \(x = - 3\), ; đạt cực tiểu tại \(x = - 1\), \({y_{CT}} = 1\).

Suy ra . Do đó, ý b) sai.

– Tiệm cận:

+) Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng \(x = - 2\).

+) Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng \(y = x + 1\).

Với \(x = 0\) thì \(y = 0 + 1 = 1\), do đó đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm \(A\left( {0;1} \right)\). Vậy ý c) đúng.

– Đường thẳng \(x - 3y - 6 = 0\)\( \Leftrightarrow y = \frac{1}{3}x - 2\) có hệ số góc \({k_1} = \frac{1}{3}\). Đường thẳng này vuông góc với tiếp tuyến của đồ thị hàm số đã cho nên tiếp tuyến này có hệ số góc \({k_2} = \frac{{ - 1}}{{{k_1}}} = - 3\).

Khi đó, với \({x_0}\) là hoành độ của tiếp điểm thì \(y'\left( {{x_0}} \right) = \frac{{x_0^2 + 4{x_0} + 2}}{{{{\left( {{x_0} + 2} \right)}^2}}} = - 3\).

Ta tìm được \({x_0} = - \frac{5}{2}\) hoặc \({x_0} = - \frac{3}{2}\).

+) Với \({x_0} = - \frac{5}{2}\), ta có tiếp tuyến: \(y = - 3x - 11\).

+) Với \({x_0} = - \frac{3}{2}\), ta có tiếp tuyến: \(y = - 3x - 3\), tiếp tuyến này đi qua điểm \(B\left( { - \frac{3}{2};\frac{3}{2}} \right)\).

Do đó, ý d) đúng.

Câu 2

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có đồ thị như hình dưới đây.

a) Hàm số đã cho nghịch biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {1;2} \right)\).

b) Hàm số đã cho có \(2\) điểm cực trị.

c) Trên đoạn \(\left[ { - 1;\,1} \right]\), giá trị lớn nhất của hàm số đã cho bằng \(2\).

d) Phương trình \(3f\left( x \right) - 6 = 0\) có duy nhất 1 nghiệm.

Xem đáp án

Lời giải

a) S, b) Đ, c) Đ, d) S.

Hướng dẫn giải

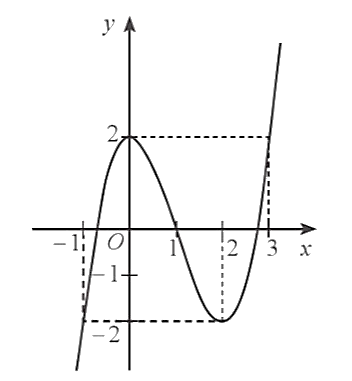
Quan sát đồ thị, ta thấy:

– Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ;\,0} \right)\) và \(\left( {2; + \infty } \right)\); nghịch biến trên khoảng \(\left( {0;2} \right)\). Vậy ý a) sai.

– Hàm số đã cho có \(2\) điểm cực trị: \(x = 0\) (điểm cực đại) và \(x = 2\) (điểm cực tiểu). Do đó, ý b) đúng.

– Trên đoạn \(\left[ { - 1;\,1} \right]\), hàm số đạt giá trị lớn nhất tại \(x = 0\), \(\mathop {\max }\limits_{\left[ { - 1;\,1} \right]} f\left( x \right) = f\left( 0 \right) = 2\). Do đó, ý c) đúng.

– Ta có \(3f\left( x \right) - 6 = 0\)\( \Leftrightarrow f\left( x \right) = 2\).

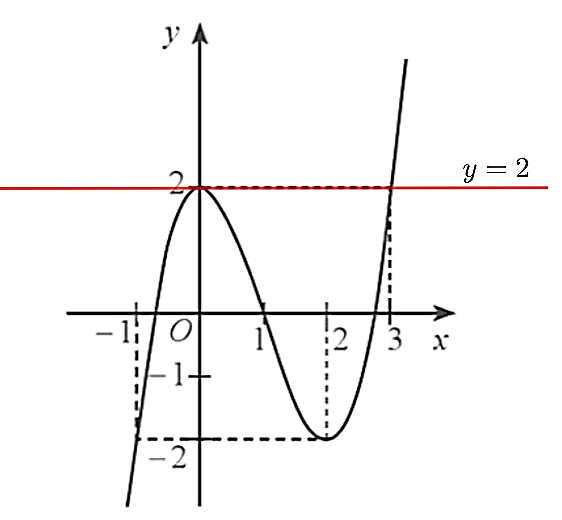
Đường thẳng \(y = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 2 điểm nên phương trình \(f\left( x \right) = 2\)có 2 nghiệm, tức là phương trình \(3f\left( x \right) - 6 = 0\) có 2 nghiệm.

Vậy ý d) sai.

Câu 3