Cho hình chóp \(S.ABC\) có \(\overrightarrow {SA} = \overrightarrow a ,\,\,\overrightarrow {SB} = \overrightarrow b ,\,\overrightarrow {SC} = \overrightarrow c \) và các điểm \(M,\,N\) lần lượt là trung điểm của các cạnh \(AB,\,SC\). Các điểm \(P,\,Q\) nằm trên các đường thẳng \(SA,\,BN\) sao cho \(PQ\,{\rm{//}}\,CM\). Khi biểu diễn vectơ \(\overrightarrow {PQ} \) theo ba vectơ \(\overrightarrow a ,\,\overrightarrow b ,\,\overrightarrow c \), ta được: \(\overrightarrow {PQ} = - \frac{m}{n}\overrightarrow a - \frac{p}{q}\overrightarrow b + \frac{r}{z}\overrightarrow c \) (với \(\frac{m}{n},\,\frac{p}{q},\,\frac{r}{z}\) là các phân số tối giản và \(m,n,p,q,r,z \in \mathbb{Z}\)). Giá trị của biểu thức \(\frac{m}{n} + \frac{p}{q} + \frac{r}{z}\) bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
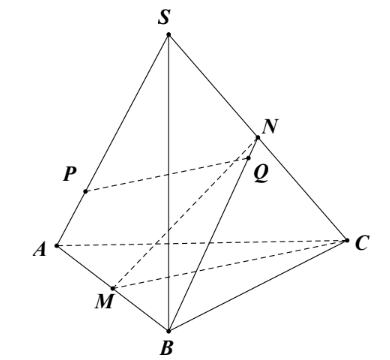
Đặt \(\overrightarrow {PA} = x\overrightarrow {SA} ,\,\,\overrightarrow {BQ} = y\overrightarrow {BN} \).
Khi đó, \(\overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AB} + \overrightarrow {BQ} = x\overrightarrow {SA} + \left( {\overrightarrow {SB} - \overrightarrow {SA} } \right) + y\left( {\overrightarrow {SN} - \overrightarrow {SB} } \right)\)
\( = \left( {x - 1} \right)\overrightarrow {SA} + \left( {1 - y} \right)\overrightarrow {SB} + y\overrightarrow {SN} \)\( = \left( {x - 1} \right)\overrightarrow {SA} + \left( {1 - y} \right)\overrightarrow {SB} + \frac{y}{2}\overrightarrow {SC} \)
\( = \left( {x - 1} \right)\overrightarrow a + \left( {1 - y} \right)\overrightarrow b + \frac{y}{2}\overrightarrow c \).
Lại có \(\overrightarrow {CM} = \overrightarrow {SM} - \overrightarrow {SC} = \frac{1}{2}\left( {\overrightarrow {SA} + \overrightarrow {SB} } \right) - \overrightarrow {SC} = \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b - \overrightarrow c \).
Vì \(PQ\,{\rm{//}}\,CM\) nên tồn tại số thực \(k \ne 0\) sao cho \(\overrightarrow {PQ} = k\overrightarrow {CM} \).
Suy ra \(\frac{{x - 1}}{{\frac{1}{2}}} = \frac{{1 - y}}{{\frac{1}{2}}} = \frac{{\frac{y}{2}}}{{ - 1}}\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \frac{2}{3}\\y = \frac{4}{3}\end{array} \right.\).
Khi đó, \(\overrightarrow {PQ} = - \frac{1}{3}\overrightarrow a - \frac{1}{3}\overrightarrow b + \frac{2}{3}\overrightarrow c \). Vậy \(\frac{m}{n} + \frac{p}{q} + \frac{r}{z} = \frac{1}{3} + \frac{1}{3} + \frac{2}{3} = \frac{4}{3} \approx 1,3\).
Đáp số: \(1,3\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: A
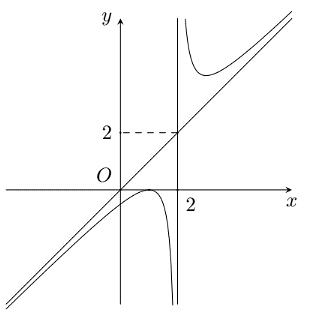
Đồ thị hàm số đã cho nhận giao điểm của hai đường tiệm cận làm tâm đối xứng.
Dựa vào đồ thị, ta thấy, giao điểm này có tọa độ là \(\left( {2;\,2} \right)\).
Lời giải
Diện tích của đáy bể là: \(S = \frac{V}{h} = \frac{{96\,\,000}}{{60}} = 1\,600\) cm2 \( = 0,16\) m2.
Gọi chiều dài đáy của bể là \(x\) (m, \(x > 0\)).
Chiều rộng đáy của bể là \(\frac{{0,16}}{x}\) (m).
Chi phí để hoàn thành bể cá là:
\(F\left( x \right) = 0,16 \cdot 100\,000 + 2 \cdot 0,6 \cdot x \cdot 70\,000 + 2 \cdot 0,6 \cdot \frac{{0,16}}{x} \cdot 70\,000\)
\( = 16\,000 + 84\,000x + \frac{{13\,440}}{x}\)(đồng).
Xét hàm số \(F\left( x \right) = 16\,000 + 84\,000x + \frac{{13\,440}}{x}\) với \(x \in \left( {0;\, + \infty } \right)\).
Ta có: \(F'\left( x \right) = 84\,000 - \frac{{13\,440}}{{{x^2}}}\). Trên khoảng \(\left( {0; + \infty } \right)\), \(F'\left( x \right) = 0 \Leftrightarrow x = 0,4\).
Bảng biến thiên của hàm số \(F\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\) như sau:
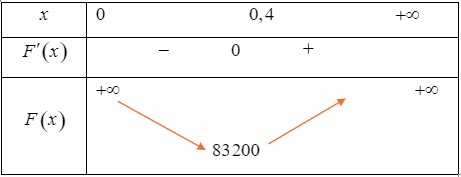
Căn cứ vào bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} F\left( x \right) = F\left( {0,4} \right) = 83\,200\).
Vậy chi phí thấp nhất để hoàn thành bể cá là \(83\,200\) đồng = \(83,2\) nghìn đồng.
Đáp số: \(83,2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.