Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \(100^\circ \) và có độ lớn lần lượt là \(25N\) và \(12N\). Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(4N\). Tính độ lớn của hợp lực của ba lực trên (Làm tròn kết quả đến hàng đơn vị).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
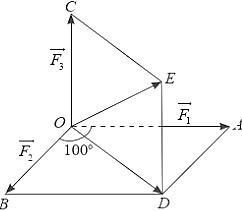
Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) là ba lực tác động vào vật tại điểm \(O\) lần lượt có độ lớn \(25N,12N,4N\).
Vẽ \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} ,\overrightarrow {OC} = \overrightarrow {{F_3}} \).
Dựng hình bình hành \(OADB\) và hình bình hành \(ODEC\).
Hợp lực tác động vào vật là:
\(\overrightarrow F = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} .\)
Áp dụng định lí côsin trong tam giác \(OBD\), ta có:
\(O{D^2} = B{D^2} + O{B^2} - 2.BD.OB.\cos \widehat {OBD} = O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \)
Vì \(OC \bot \left( {OADB} \right)\) nên \(OC \bot OD\), suy ra \(ODEC\) là hình chữ nhật.
Do đó, tam giác \(DOE\) vuông tại \(D\).
Ta có: \(O{E^2} = O{C^2} + O{D^2} = O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ \).
Suy ra:
\(OE = \sqrt {O{C^2} + O{A^2} + O{B^2} + 2.OA.OB.\cos 100^\circ } \)\( = \sqrt {{4^2} + {{25}^2} + {{12}^2} + 2.25.12.\cos 100^\circ } \)
\(OE \approx 26N\).
Vậy độ lớn của hợp lực \(F = OE \approx 26N\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: B
Gọi điểm \(M\) thuộc trục \(Ox\) có tọa độ \(\left( {x;0;0} \right)\).
Theo đề, ta có \(M\) cách đều hai điểm \(A\left( {4;2; - 1} \right)\) và \(B\left( {2;1;0} \right)\) hay \(MA = MB\).
Ta có: \(MA = MB\) \( \Rightarrow \)\(M{A^2} = M{B^2}\)
\( \Leftrightarrow {\left( {x - 4} \right)^2} + {(0 - 2)^2} + {\left[ {0 - \left( { - 1} \right)} \right]^2} = {\left( {2 - x} \right)^2} + {\left( {1 - 0} \right)^2} + {\left( {0 - 0} \right)^2}\)
\( \Leftrightarrow {x^2} - 8x + 16 + 4 + 1 = {x^2} - 4x + 4 + 1\)
\( \Leftrightarrow 4x = 16\)
\( \Leftrightarrow x = 4.\)
Vậy \(M\left( {4;0;0} \right)\).
Câu 2
Lời giải
Đáp án đúng là: B
Ta có: \(V(T) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}.\)
\( \Rightarrow V'\left( T \right) = - 0,06426 + 0,0170086T - 2,{037.10^{ - 4}}{T^2}\)
\(V'\left( T \right) = 0 \Leftrightarrow - 2,{037.10^{ - 4}}{T^2} + 0,0170086T - 0,06426 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}T \approx 79,53\,\,\,\,(L)\\T \approx 3,97\,\,\,\,\,(TM)\end{array} \right.\).
Ta có bảng xét dấu như sau:
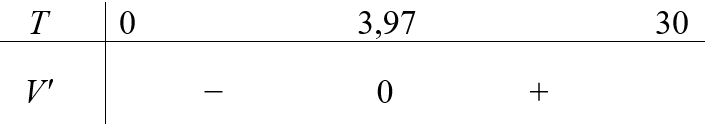
Vậy thể tích giảm khi \(T \in \left( {0^\circ C;3,97^\circ C} \right)\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.