Một khúc sông rộng khoảng \[130\] m. Một con đò dự định chèo từ bờ bên này sang bờ bên kia theo phương vuông góc với bờ sông, nhưng do bị dòng nước đẩy xiên nên phải chèo khoảng \[150\] m mới sang được bờ bên kia (hình vẽ).
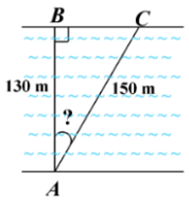
Khi đó dòng nước đã đẩy con đò đi lệch một góc khoảng bao nhiêu độ so với phương dự định ban đầu?
A. \[30^\circ.\]
B. \[40^\circ.\]
C. \[50^\circ.\]
D. \[60^\circ.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Ta có dòng nước đã đẩy con đò đi lệch một góc \[\widehat {BAC}\] so với dự định ban đầu.
Theo đề, ta có \[BA = 130\] (m) và \[AC = 150\] (m).
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\cos \widehat {BAC} = \frac{{BA}}{{AC}} = \frac{{130}}{{150}} = \frac{{13}}{{15}}.\]
Suy ra \[\widehat {BAC} \approx 30^\circ .\]
Do đó dòng nước đã đẩy con đò đi lệch một góc \[30^\circ \] so với phương dự định ban đầu.
Vậy ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[2\,\,716\] mét.
B. \[2\,\,301\] mét.
C. \[977\] mét.
D. \[6\,\,398\] mét.
Lời giải
Đáp án đúng là: D
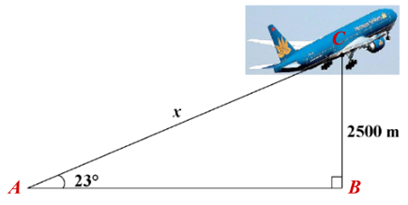
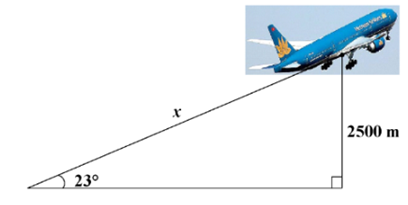
Theo đề, ta có \[\widehat {BAC} = 23^\circ \] và \[BC = 2\,\,500\] (m).
Vì tam giác \[ABC\] vuông tại \[B\] nên \[\sin \widehat {BAC} = \frac{{BC}}{{AC}}.\]
Suy ra \[AC = \frac{{BC}}{{\sin \widehat {BAC}}}\] hay \[x = \frac{{2\,\,500}}{{\sin 23^\circ }} \approx 6\,\,398\] (m).
Do đó muốn đạt độ cao \[2500\] m thì máy bay phải bay một đoạn đường \[x\] dài \[6\,\,398\] mét.
Vậy ta chọn phương án D.
Câu 2
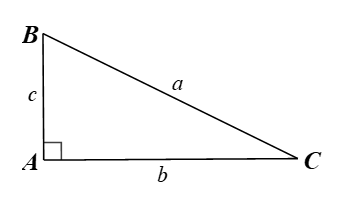
A. \[BC = \sqrt {74} {\rm{\;cm}};\,\,\widehat C \approx 35^\circ 32'.\]
B. \[BC = \sqrt {74} {\rm{\;cm}};\,\,\widehat C \approx 54^\circ 28'.\]
C. \[BC = 2\sqrt 6 {\rm{\;cm}};\,\,\widehat {C\,} \approx 35^\circ 32'.\]
D. \[BC = 2\sqrt 6 {\rm{\;cm}};\,\,\widehat C \approx 54^\circ 28'.\]
Lời giải
Đáp án đúng là: A
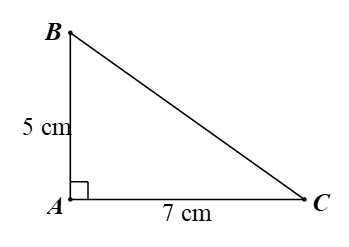
Xét tam giác \[ABC\] vuông tại \[A\], có: \[B{C^2} = A{B^2} + A{C^2}\] (Định lí Pythagore)
Suy ra \[B{C^2} = A{B^2} + A{C^2} = {5^2} + {7^2} = 74.\] Do đó \[BC = \sqrt {74} \] (cm).
Vì tam giác \[ABC\] vuông tại \[A\] nên \[\tan C = \frac{{AB}}{{AC}} = \frac{5}{7}.\]
Suy ra \[\widehat C \approx 35^\circ 32'.\]
Vậy ta chọn phương án A.
Câu 3
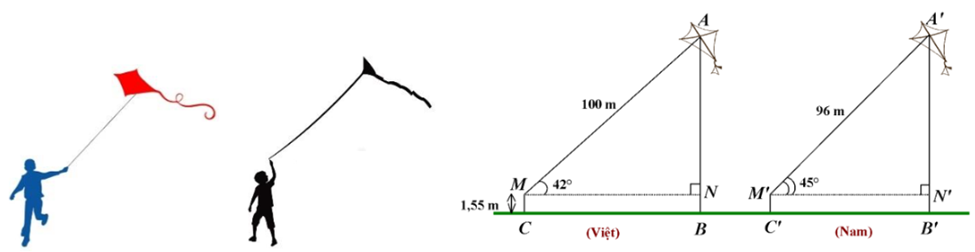
A. So với mặt đất thì diều của bạn Việt lên cao hơn diều của bạn Nam và cao hơn \[0,25\] m.
B. So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[0,97\] m.
C. So với mặt đất thì diều của bạn Nam lên cao hơn diều của bạn Việt và cao hơn \[1,03\] m.
D. So với mặt đất thì diều của hai bạn Việt và Nam lên cao bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[5\] (đvdt).
B. \[4\] (đvdt).
C. \[3\] (đvdt).
D. \[2\] (đvdt).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
![Một khúc sông rộng khoảng \[250\] m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng \[320\] m mới sang được bờ bên kia. Giả sử dòng nước đã đẩy con đò đi lệch một góc \[\ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729481212.png)
A. sin.
B. côsin.
C. tang.
D. côtang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[c = a.\cot B.\]
B. \[c = a.\sin B.\]
C. \[c = a.\tan B.\]
D. \[c = a.\cos B.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo