khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Đánh giá năng lực
  3. ĐH Bách Khoa

Câu hỏi:

23/10/2024 443 Lưu

Một số nước phương Đông, trong đó có Việt Nam gọi tên năm Âm lịch bằng cách ghép tên của 1 trong 10 can với tên của 1 trong 12 chi.

CAN

Giáp

Ất

Bính

Đinh

Mậu

Kỉ

Canh

Tân

Nhâm

Quý

Giáp

Ất

CHI

Tý

Sửu

Dần

Mão

Thìn

Tỵ

Ngọ

Mùi

Thân

Thân

Tuất

Hợi

Ví dụ Giáp được ghép với Tý thành năm Giáp Tý, Ất được ghép với Sửu thành năm Ất Sửu, … Cứ lặp lại vòng tuần hoàn như thế thì tối thiểu sau bao nhiêu năm thì năm Quý Mão được lặp lại? Tại sao?

A. Vì cứ 10 năm, can Quý được lặp lại và cứ 12 năm, chi Mão được lặp lại, nên số năm Quý Mão được lặp lại là bội chung của 10 và 12 và bằng 60.

B. Vì cứ 10 năm, can Quý được lặp lại và cứ 12 năm, chi Mão được lặp lại, nên số năm Quý Mão được lặp lại là tích của 10 và 12 và bằng 120.

C. Vì cứ 10 năm, can Quý được lặp lại. Cứ 12 năm, chi Mão được lặp lại, nên số năm Quý Mão được lặp lại là tích của các thừa số nguyên tố chung và riêng của 10 và 12 là 2, 3, 5 và bằng 30.

D. Vì cứ 10 năm, can Quý được lặp lại và cứ 12 năm, chi Mão được lặp lại, nên số năm Quý Mão được lặp lại là bội chung của 10 và 12. Và số năm tối thiểu năm Quý Mão lặp lại là bội chung nhỏ nhất của 10 và 12 và bằng 60.
Xem lời giải

Câu hỏi trong đề: Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 5) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Giải thích

Vì cứ 10 năm, can Quý được lặp lại. Cứ 12 năm, chi Mão được lặp lại, nên số năm Quý Mão được lặp lại là bội chung của 10 và 12. Và số năm ít nhất năm Quý Mão lặp lại là bội chung nhỏ nhất của 10 và 12.

Phân tích 10 và 12 ra thừa số nguyên tố ta được: 10 = 2.5 và 12 = 22.3.

Các thừa số nguyên tố chung và riêng của 10 và 12 là 2, 3, 5 với số mũ lớn nhất lần lượt là: 2, 1, 1.

Khi đó: BCNN (10,12)=22.3.5 = 60.

Vậy cứ sau 60 năm thì năm Quý Mão được lặp lại.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} + 4x - 6y + m = 0\) (\(m\) là tham số) và đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 4 + 2t}\\{y = 3 + t}\\{z = 3 + 2t}\end{array}} \right.\). Biết đường thẳng \(\Delta \) cắt mặt cầu \((S)\) tại hai điểm phân biệt A, B sao cho \(AB = 8.\) Giá trị của tham số \(m\) thuộc khoảng nào trong các khoảng dưới đây? 
A. (−10;0).                   
B. (−12;−3).                  
C. (−8;2).    
D. (−15;−5).

Lời giải

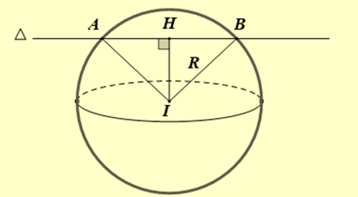
Media VietJack

Gọi \(H\) là trung điểm đoạn thẳng \(AB \Rightarrow IH \bot AB,HA = 4\).

Mặt cầu \((S)\) có tâm \(I( - 2;3;0)\), bán kính \(R = \sqrt {13 - m} ,\,\,(m < 13)\).

Đường thẳng \(\Delta \) đi qua \(M(4;3;3)\) và có 1 vectơ chỉ phương \(\vec u = (2;1;2)\).

Ta có: \(\overrightarrow {IM}  = (6;0;3) \Rightarrow [\overrightarrow {IM} ,\vec u] = ( - 3; - 6;6) \Rightarrow IH = d(I,\Delta ) = \frac{{\left| {\left[ {\overrightarrow {IM} ,\vec u} \right]} \right|}}{{|\vec u|}} = 3\)

\( \Rightarrow {R^2} = I{H^2} + H{A^2} \Leftrightarrow 13 - m = {3^2} + {4^2} \Leftrightarrow m =  - 12\).

Vậy tham số \(m\) thuộc \(( - 15; - 5)\). 

Câu 2

Một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau 5 phút người ta đếm được có 64000 con. Hỏi sau bao nhiêu phút thì có được 2048000 con?
A. 8 phút.                      
B. 9 phút.                     
C. 11 phút.    
D. 10 phút.

Lời giải

Số lượng vi khuẩn tăng sau mỗi phút lên là cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q = 2\). Ta có: \({u_6} = 64000 \Rightarrow {u_1}.{q^5} = 64000 \Rightarrow {u_1} = 2000\).

Sau \(n\) phút thì số lượng vi khuẩn là \({u_{n + 1}}\).

\({u_{n + 1}} = 2048000 \Rightarrow {u_1}.{q^n} = 2048000 \Rightarrow {2000.2^n} = 2048000 \Rightarrow n = 10.{\rm{ }}\)

Vậy sau 10 phút thì có được 2048000 con.

Câu 3

Một quả bóng cao su được thả từ độ cao 5 mét xuống một mặt sàn. Sau mỗi lần chạm sàn, quả bóng nảy lên độ cao bằng \(\frac{2}{3}\) độ cao trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Tổng các quãng đường khi rơi và nảy của quả bóng từ lúc thả bóng cho đến lúc bóng không nảy lên nữa là
A. 15 m.                        
B. 10 m.                        
C. 20 m.    
D. 25 m.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Chia ngẫu nhiên 20 hộp bánh giống nhau thành 4 phần quà (phần nào cũng có bánh). Có bao nhiêu cách chia để mỗi phần quà đều có ít nhất 3 hộp bánh.
A. 220.                         
B. 495.                          
C. 330.    
D. 165.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Phát biểu sau đây đúng hay sai? 

Xét cùng một loại khí tại cùng điều kiện áp suất và nhiệt độ, thể tích khí tăng thì khối lượng khí tăng.

A. Đúng

B. Sai

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Kéo các ô vuông thả vào vị trí thích hợp trong các câu sau:

Media VietJack

Một chiếc ô tô đang đi trên đường với vận tốc \(v(t) = 3t - 15\,\,(t \ge 3)\,\,({\rm{m}}/{\rm{s}})\), trong đó t là khoảng thời gian tính bằng giây. Quãng đường ô tô đi được trong 10 giây bắt đầu từ thời điểm t = 3 là: _______ (m)

Khi ô tô đạt vận tốc \(30\;{\rm{m}}/{\rm{s}}\) thì người lái xe phát hiện có hàng rào chắn ngang đường ở phía trước cách xe 100 m (tính từ đầu xe tới hàng rào) nên người lái đạp phanh. Từ thời điểm đó, xe chuyển động chậm dần đều với vận tốc \(v(t) =  - 5t + 100(\;{\rm{m}}/{\rm{s}})\). Từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển _______ (m).

Khi xe dừng hẳn, khoảng cách từ xe đến hàng rào là _______ (m).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

bao nhiêu giá trị nguyên dương nhỏ hơn 10 của tham số \(m\) để hàm số \(y = \frac{{ - mx + 6}}{{x - m}}\) đồng biến trên khoảng \(( - 2;2)\)?
A. 10.                           
B. 8.                             
C. 6.    
D. 7

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập