Câu hỏi:
23/10/2024 268Tập hợp tất cả các giá trị thực của tham số \(m\) để bất phương trình \({\log _4}\left( {{x^2} - x - m} \right) \ge {\log _2}(x - 2)\) có nghiệm với mọi giá trị \(x\) thuộc tập xác định là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Điều kiện: \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - x - m > 0}\\{x - 2 > 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - x - m > 0}\\{x > 2}\end{array}} \right.} \right.\)
Với điều kiện trên bất phương trình đã cho tương đương với
\({\log _4}\left( {{x^2} - x - m} \right) \ge {\log _2}(x - 2) \Leftrightarrow {\log _2}\left( {{x^2} - x - m} \right) \ge {\log _2}{(x - 2)^2}\)
\( \Leftrightarrow {x^2} - x - m \ge {x^2} - 4x + 4 \Leftrightarrow m \le 3x - 4(**).\)
Khi đó, \({x^2} - x - m > 0 \Leftrightarrow {x^2} - x - m \ge {x^2} - x - 3x + 4 = {x^2} - 4x + 4 = {(x - 2)^2} > 0\) (vì \(x > 2\) ).
Vậy bất phương trình đã cho có nghiệm với mọi giá trị \(x\) thuộc tập xác định khi \((**)\) có nghiệm với mọi giá trị \(x\) thuộc tập xác định \( \Leftrightarrow m \le {\min _{(2; + \infty )}}(3x - 4) \Rightarrow m \le 2\).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
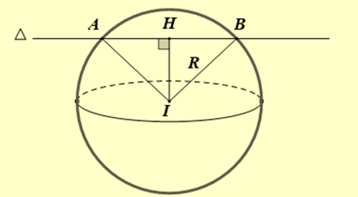
Gọi \(H\) là trung điểm đoạn thẳng \(AB \Rightarrow IH \bot AB,HA = 4\).
Mặt cầu \((S)\) có tâm \(I( - 2;3;0)\), bán kính \(R = \sqrt {13 - m} ,\,\,(m < 13)\).
Đường thẳng \(\Delta \) đi qua \(M(4;3;3)\) và có 1 vectơ chỉ phương \(\vec u = (2;1;2)\).
Ta có: \(\overrightarrow {IM} = (6;0;3) \Rightarrow [\overrightarrow {IM} ,\vec u] = ( - 3; - 6;6) \Rightarrow IH = d(I,\Delta ) = \frac{{\left| {\left[ {\overrightarrow {IM} ,\vec u} \right]} \right|}}{{|\vec u|}} = 3\)
\( \Rightarrow {R^2} = I{H^2} + H{A^2} \Leftrightarrow 13 - m = {3^2} + {4^2} \Leftrightarrow m = - 12\).
Vậy tham số \(m\) thuộc \(( - 15; - 5)\).
Lời giải
Số lượng vi khuẩn tăng sau mỗi phút lên là cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q = 2\). Ta có: \({u_6} = 64000 \Rightarrow {u_1}.{q^5} = 64000 \Rightarrow {u_1} = 2000\).
Sau \(n\) phút thì số lượng vi khuẩn là \({u_{n + 1}}\).
\({u_{n + 1}} = 2048000 \Rightarrow {u_1}.{q^n} = 2048000 \Rightarrow {2000.2^n} = 2048000 \Rightarrow n = 10.{\rm{ }}\)
Vậy sau 10 phút thì có được 2048000 con.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 29)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 8)