Câu hỏi:
26/10/2024 280
Gọi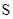 
là tập hợp các giá trị nguyên của 
để hàm số 
đồng biến trên một khoảng có độ dài nhỏ hơn 1 .
Số phần tử của S là _______.
Gọi là tập hợp các giá trị nguyên của để hàm số đồng biến trên một khoảng có độ dài nhỏ hơn 1 .
Số phần tử của S là _______.
Quảng cáo
Trả lời:
Giải bởi Vietjack
ТХÐ: 
.
Ta có: 
Nếu 
Hàm số nghịch biến trên 
nên hàm số không có khoảng đồng biến.
Nếu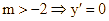 
có hai nghiệm 
, và 
Yêu cầu bài toán 
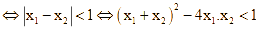
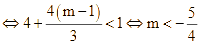
Vậy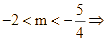 
Có 0 giá trị nguyên của 
thỏa mãn bài toán.
Do đó ta điền đáp án như sau
Gọi 
là tập hợp các giá trị nguyên của để hàm số đồng biến trên một khoảng có độ dài nhỏ hơn 1 .
Số phần tử của S là 0.
Sách thầy cô Vietjack biên soạn:
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 290.000
₫ 140.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1)
Đã bán 851
₫ 150.000
₫ 39.000
Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1)
Đã bán 902
₫ 150.000
₫ 39.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một kĩ sư mới ra trường làm việc với mức lương khởi điểm là 7 triệu đồng/tháng. Cứ sau 9 tháng làm việc, mức lương của kĩ sư đó lại được tăng thêm 10%. Hỏi sau 4 năm làm việc, tổng số tiền lương kĩ sư đó nhận được là bao nhiêu?
Xem đáp án »
26/10/2024
1,487
Câu 2:
Chọn đáp án chính xác nhất.
Cơ thể vi khuẩn được cấu tạo từ dạng tế bào nào?
Chọn đáp án chính xác nhất.
Cơ thể vi khuẩn được cấu tạo từ dạng tế bào nào?
Xem đáp án »
26/10/2024
1,256
Câu 3:
Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây. Người ta đo được đường kính của miệng ly là 
và chiều cao là 
. Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng đối xứng là một parabol.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Diện tích thiết diện là _______.
Tính thể tích của vật thể đã cho là V = _______.
Có một vật thể là hình tròn xoay có dạng giống như một cái ly như hình vẽ dưới đây. Người ta đo được đường kính của miệng ly là và chiều cao là . Biết rằng thiết diện của chiếc ly cắt bởi mặt phẳng đối xứng là một parabol.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Diện tích thiết diện là _______.
Tính thể tích của vật thể đã cho là V = _______.
Xem đáp án »
26/10/2024
1,011
Câu 4:
Cho hàm số 
xác định trên 
.
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Giá trị lớn nhất của 
là _______.
Cho 
, số nghiệm của phương trình 
là: _______.
Số điểm biểu diễn nghiệm của bất phương trình 
trên đường tròn lượng giác là _______.
Cho hàm số xác định trên .
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau:
Giá trị lớn nhất của là _______.
Cho , số nghiệm của phương trình là: _______.
Số điểm biểu diễn nghiệm của bất phương trình trên đường tròn lượng giác là _______.
Xem đáp án »
26/10/2024
760
Câu 5:
Vì sao các nhà khoa học Việt cần nghiên cứu và chế tạo ra pin sạc Li-ion?
Xem đáp án »
26/10/2024
701
Câu 6:
Tại sao vấn đề dân tộc được coi là một trong những vấn đề quan trọng nhất trong nghiên cứu lịch sử?
Xem đáp án »
26/10/2024
641
Câu 7:
Dựa trên thông tin trong Bảng 1, để xác định chính xác ion kim loại bằng sắc ký giấy, người ta cần biết
Xem đáp án »
26/10/2024
639
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận