Tổng tất cả các giá trị thực của tham số \(m\) để khoảng cách từ điểm \(M\left( {0;3} \right)\) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \(y = {x^3} + 3mx + 1\) bằng \(\frac{2}{{\sqrt 5 }}\) là (1) ________.
Tổng tất cả các giá trị thực của tham số \(m\) để khoảng cách từ điểm \(M\left( {0;3} \right)\) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \(y = {x^3} + 3mx + 1\) bằng \(\frac{2}{{\sqrt 5 }}\) là (1) ________.
Quảng cáo
Trả lời:
Đáp án
Tổng tất cả các giá trị thực của tham số \(m\) để khoảng cách từ điểm \(M\left( {0;3} \right)\) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số \(y = {x^3} + 3mx + 1\) bằng \(\frac{2}{{\sqrt 5 }}\) là (1) ____-1____.
Giải thích
Ta có \(y' = 3{x^2} + 3m;y' = 0 \Leftrightarrow {x^2} = - m\).
Hàm số có hai điểm cực trị \( \Leftrightarrow y' = 0\) có hai nghiệm phân biệt \( \Leftrightarrow m < 0\). \(\left( {\rm{*}} \right)\)
Thực hiện phép chia \(y\) cho \(y'\) ta được phần dư \(2mx + 1\), nên đường thẳng \({\rm{\Delta }}:y = 2mx + 1\) chính là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.
Yêu cầu bài toán \( \Leftrightarrow d\left( {M,{\rm{\Delta }}} \right) = \frac{2}{{\sqrt {4{m^2} + 1} }} = \frac{2}{{\sqrt 5 }} \Leftrightarrow {m^2} = 1 \Leftrightarrow m = \pm 1\).
Đối chiếu điều kiện \(\left( {\rm{*}} \right)\), ta có \(m = - 1\) thỏa mãn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
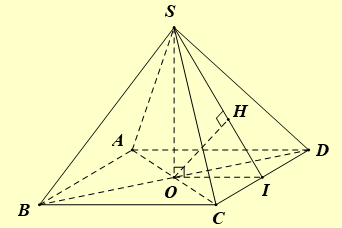
Vì \(I\) là trung điểm của \(CD \Rightarrow OI \bot CD,CD = 2OI\).
Kẻ \(OH \bot SI\) tại \(H \Rightarrow OH \bot \left( {SCD} \right) \Rightarrow d\left( {O,\left( {SCD} \right)} \right) = d\left( {O,SI} \right) = OH = 1\).
Ta có \(\left\{ {\begin{array}{*{20}{l}}{(SCD) \cap (ABCD) = CD}\\{SI \subset (SCD),SI \bot CD}\\{OI \subset (ABCD),OI \bot CD}\end{array}} \right. \Rightarrow ((SCD),(ABCD)) = (SI,OI) = (SI,AD) = \widehat {SIO} = {45^^\circ }\)
Xét tam giác vuông \(HIO \Rightarrow OI = \frac{{OH}}{{{\rm{sin}}\widehat {SIO}}} = \frac{1}{{{\rm{sin}}{{45}^ \circ }}} = \sqrt 2 \Rightarrow CD = 2OI = 2\sqrt 2 \).
Ta có \({\rm{\Delta }}SIO\) là tam giác vuông cân tại \(O \Rightarrow SO = OI = \sqrt 2 \).
Vậy \({V_{S.ABCD}} = \frac{1}{3}C{D^2}.SO = \frac{1}{3}{(2\sqrt 2 )^2}.\sqrt 2 = \frac{{8\sqrt 2 }}{3}\).
Chọn D
Lời giải
Văn bản đã cung cấp thông tin “Các liên kết bền hơn cần được cung cấp nhiệt độ cao hơn để phá vỡ liên kết đó”.
Chọn A
Câu 3
A. Lắp đặt hệ thống mái che tại các khu vực công cộng.
B. Xây dựng hệ thống tự cân bằng nhiệt trên đường phố.
C. Thiết kế hệ thống mái che tự động tại trạm xe buýt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Có bao nhiêu cách chia 100 chiếc kẹo giống nhau cho 12 em nhỏ sao cho mỗi em có ít nhất 8 chiếc kẹo?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
