Gọi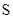 
là tập hợp tất cả các giá trị nguyên dương của tham số 
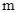để bất phương trình 
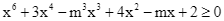đúng với mọi 
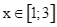. Tổng của tất cả các phần tử thuộc 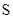bằng:
là tập hợp tất cả các giá trị nguyên dương của tham số để bất phương trình đúng với mọi . Tổng của tất cả các phần tử thuộc bằng:A. 
.
.B. 2.
C. 
.
.D. 
.
.Quảng cáo
Trả lời:
Giải bởi Vietjack
Bất phương trình đã cho đúng với mọi 
, 
.
Xét hàm số: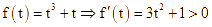 
. Vậy 
đồng biến trên 
.
Suy ra bất phương trình đã cho đúng với mọi
.
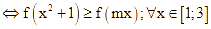
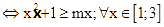
Vì tham số 
nguyên dương suy ra 
.
Vậy tổng tất cả các phần tử thuộc 
bằng 
. Chọn A.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 0,176.
B. 0,88.
C. 1,76.
D. 0,44.
Lời giải
; 
Số mol 
đem đi chuẩn độ là: 0,001a (mol)
PTHH: 
Bảo toàn electron ta có: 
→ a = 0,88
Chọn B.
Câu 2
A. Nhiệt độ trung bình tháng VII cao nhất ở Huế vì chịu tác động mạnh mẽ của gió phơn khô nóng.
B. Ở TP. Hồ Chí Minh, nhiệt độ tháng VII thấp hơn các địa điểm khác vì đây là tháng có mưa lớn.
C. Nhiệt độ trung bình năm tăng dần từ Bắc vào Nam vì càng về phía Nam góc nhập xạ càng lớn, lượng nhiệt nhận được càng nhiều.
D. Tháng I, chênh lệch nhiệt độ giữa 2 miền Bắc Nam rõ rệt do miền Bắc chịu ảnh hưởng của gió mùa Đông Nam lạnh.
Lời giải
Tháng I, chênh lệch nhiệt độ giữa 2 miền Bắc Nam rõ rệt do miền Bắc chịu ảnh hưởng của gió mùa Đông Bắc lạnh. → Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 178.103 MeV.
B. 1,78.103 MeV.
. C. 17,8.103 MeV.
D. 0,178.103 MeV.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. tiền phạt (6 triệu - 8 triệu), tước giấy phép lái xe (22 - 24 tháng).
B. tiền phạt (2 triệu - 3 triệu), tước giấy phép lái xe (10 - 12 tháng).
C. tiền phạt (4 triệu - 5 triệu), tước giấy phép lái xe (16 - 18 tháng).
D. tiền phạt (2 triệu - 3 triệu), tước giấy phép lái xe (16 - 18 tháng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo