People realized they had misunderstood her when they labeled her as a villain. She was truly desperate to prove herself.
A. Only by she was truly desperate to prove herself did people realize they had misunderstood her when they labeled her as a villain.
D. Had people realized they had misunderstood her when they labeled her as a villain, she would have been truly desperate to prove herself.
Quảng cáo
Trả lời:
Kiến thức về câu đảo ngữ
Dịch: Mọi người nhận ra họ đã hiểu lầm khi gán cho cô ấy là kẻ phản diện. Cô ấy thực sự tuyệt vọng muốn chứng minh bản thân.
A. Chỉ bằng cách cô ấy thực sự tuyệt vọng muốn chứng minh bản thân thì mọi người mới nhận ra họ đã hiểu lầm khi gán cho cô ấy là kẻ phản diện. → Sai nghĩa và ngữ pháp. Cấu trúc đảo ngữ: Only by + N/V-ing + trợ động từ + S + V-inf + O: Chỉ bằng cách…thì…
B. Mãi cho đến khi mọi người nhận ra họ đã hiểu lầm khi gán cho cô ấy là kẻ phản diện thì cô ấy mới thực sự tuyệt vọng muốn chứng minh bản thân. → Sai nghĩa. Cấu trúc đảo ngữ: Not until + S + had + Vp2/V-ed + O + did + S + V-inf + O: Mãi cho đến khi…thì…
C. Mãi cho đến khi cô ấy thực sự tuyệt vọng muốn chứng minh bản thân thì mọi người mới nhận ra họ đã hiểu lầm khi gán cho cô ấy là kẻ phản diện. → Đúng. Cấu trúc đảo ngữ: Not until + S + V + O + trợ động từ + S + V-inf + O: Mãi cho đến khi…thì…
D. Nếu mọi người nhận ra họ đã hiểu lầm khi gán cho cô ấy là kẻ phản diện, cô ấy sẽ thực sự tuyệt vọng muốn chứng minh bản thân. → Sai nghĩa. Cấu trúc đảo ngữ câu điều kiện loại 3: Had + S + Vp2/V-ed + O, S + would/could/should + have + Vp2/V-ed + O: Diễn tả một hành động/sự vật/sự việc không xảy ra trong quá khứ.
Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
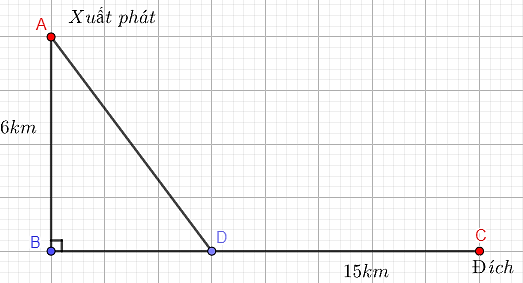
Giả sử 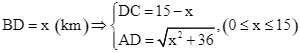 .
.
Tổng thời gian để vận động viên về đích là 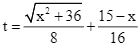 (giờ).
(giờ).
Xét hàm số 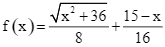 ,
,![]() , ta có
, ta có 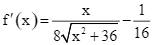 .
.
![]() .
.
Ta có bảng biến thiên:
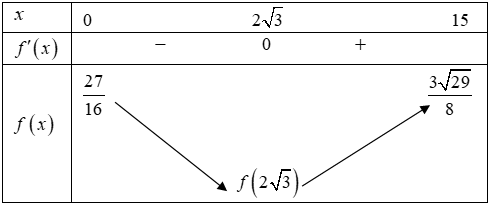
Vậy vận động viên nên vào bờ tại vị trí ![]() cách đích
cách đích ![]() một khoảng là
một khoảng là ![]() .
.
Đáp án cần nhập là: 11,54.
Lời giải
Gọi ![]() là biến cố: “Lần thứ nhất lấy được bi màu trắng”.
là biến cố: “Lần thứ nhất lấy được bi màu trắng”.
Gọi ![]() là biến cố: “Lần thứ hai lấy được bi màu đen”.
là biến cố: “Lần thứ hai lấy được bi màu đen”.
Suy ra ![]() là biến cố: “Lần thứ nhất lấy được bi màu trắng và lần thứ hai lấy được bi màu đen”.
là biến cố: “Lần thứ nhất lấy được bi màu trắng và lần thứ hai lấy được bi màu đen”.
Vì sau khi lấy viên bi thứ nhất xong, ta để lại viên bi vào bình, nên không làm ảnh hưởng xác suất lấy viên bi lần thứ hai. Ta thấy 2 biến cố ![]() và
và ![]() độc lập với nhau.
độc lập với nhau.
Xác suất để lần thứ nhất lấy được bi màu trắng là: ![]() .
.
Xác suất để lần thứ hai lấy được bi màu đen là: ![]() .
.
Áp dụng quy tắc nhân xác suất, xác suất để lấy được bi thứ 1 màu trắng và bi thứ 2 màu đen là:
![]() . Chọn B.
. Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
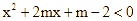 nghiệm đúng với mọi
nghiệm đúng với mọi