Câu hỏi:
10/11/2024 85
Trong không gian \(Oxyz\), cho điểm \(E\left( {2;1;3} \right)\), mặt phẳng \(\left( P \right):2x + 2y - z - 3 = 0\) và mặt cầu\(\left( S \right):{(x - 3)^2} + {(y - 2)^2} + {(z - 5)^2} = 36\). Gọi \({\rm{\Delta }}\) là đường thẳng đi qua \(E\), nằm trong \(\left( P \right)\) và cắt \(\left( S \right)\) tại hai điểm \(A\) và \(B\) có khoảng cách nhỏ nhất. Biết \({\rm{\Delta }}\) có một vectơ chỉ phương \(\vec u = \left( {2023;{y_0};{z_0}} \right)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Giá trị của \({y_0}\) bằng _______.
Giá trị của \({z_0}\) bằng _______.
Khoảng cách \(AB\) nhỏ nhất bằng \(2\sqrt a \) với \(a\) bằng _______.
Trong không gian \(Oxyz\), cho điểm \(E\left( {2;1;3} \right)\), mặt phẳng \(\left( P \right):2x + 2y - z - 3 = 0\) và mặt cầu\(\left( S \right):{(x - 3)^2} + {(y - 2)^2} + {(z - 5)^2} = 36\). Gọi \({\rm{\Delta }}\) là đường thẳng đi qua \(E\), nằm trong \(\left( P \right)\) và cắt \(\left( S \right)\) tại hai điểm \(A\) và \(B\) có khoảng cách nhỏ nhất. Biết \({\rm{\Delta }}\) có một vectơ chỉ phương \(\vec u = \left( {2023;{y_0};{z_0}} \right)\).
Kéo số ở các ô vuông thả vào vị trí thích hợp trong các câu sau
Giá trị của \({y_0}\) bằng _______.
Giá trị của \({z_0}\) bằng _______.
Khoảng cách \(AB\) nhỏ nhất bằng \(2\sqrt a \) với \(a\) bằng _______.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
Giá trị của \({y_0}\) bằng -2023.
Giá trị của \({z_0}\) bằng 0.
Khoảng cách \(AB\) nhỏ nhất bằng \(2\sqrt a \) với \(a\) bằng 30.
Giải thích
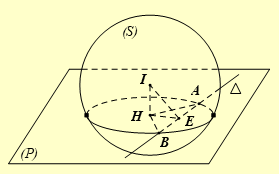
Mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến là \(\overrightarrow {{n_P}} = \left( {2;2; - 1} \right)\).
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {3;2;5} \right)\) và bán kính \(R = 6 \Rightarrow \overrightarrow {EI} = \left( {1;1;2} \right)\)
\( \Rightarrow IE = \sqrt {{1^2} + {1^2} + {2^2}} = \sqrt 6 < R \Rightarrow \) điểm \(E\) nằm trong mặt cầu \(\left( S \right)\).
Gọi \(H\) là hình chiếu của \(I\) trên mặt phẳng \(\left( P \right),A\) và \(B\) là hai giao điểm của \({\rm{\Delta }}\) với \(\left( S \right)\).
Khi đó, \(AB\) nhỏ nhất \( \Leftrightarrow d{(H;AB)_{{\rm{max}}}} \Leftrightarrow AB \bot HE\), mà \(AB \bot IH\) nên \(AB \bot \left( {HIE} \right) \Rightarrow AB \bot IE\).
Suy ra \(\overrightarrow {{u_{\rm{\Delta }}}} = \left[ {\overrightarrow {{n_P}} ;\overrightarrow {EI} } \right] = \left( {5; - 5;0} \right)\parallel \left( {1; - 1;0} \right)\) là một vectơ chỉ phương của \({\rm{\Delta }}\).
Suy ra \(\vec u = \left( {2023; - 2023;0} \right)\) là một vectơ chỉ phương của \({\rm{\Delta }}\), do đó \({y_0} = - 2023,{z_0} = 0\).
Ta có: \(IH = d\left( {I,\left( P \right)} \right) = \frac{{\left| {2.3 + 2.2 - 5 - 3} \right|}}{{\sqrt {{2^2} + {2^2} + {{( - 1)}^2}} }} = \frac{2}{3}\).
\(\Delta IHE\) vuông tại \(H:HE = \sqrt {I{E^2} - I{H^2}} = \sqrt {6 - {{\left( {\frac{2}{3}} \right)}^2}} = \frac{{5\sqrt 2 }}{3}\).
\({\rm{\Delta }}IHB\) vuông tại \(H:HB = \sqrt {I{B^2} - I{H^2}} = \sqrt {36 - {{\left( {\frac{2}{3}} \right)}^2}} = \frac{{8\sqrt 5 }}{3}\).
\(\Delta HEB\) vuông tại \(E:BE = \sqrt {H{B^2} - H{E^2}} = \sqrt {{{\left( {\frac{{8\sqrt 5 }}{3}} \right)}^2} - {{\left( {\frac{{5\sqrt 2 }}{3}} \right)}^2}} = \sqrt {30} \).
\( \Rightarrow AB = 2BE = 2\sqrt {30} \).
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo phần dẫn, ta có: Nước có thể tích xác định là do lực tương tác giữa các phân tử nước là lực hút.
Chọn B
Lời giải
Đáp án: “200/3”
Giải thích
Xét hệ trục tọa độ như hình vẽ với trục đối xứng của Parabol trùng với trục tung, trục hoành trùng với đường tiếp đất của cổng.
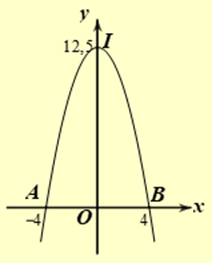
Khi đó Parabol có phương trình dạng \(y = a{x^2} + c\).
Vì \(\left( P \right)\) đi qua đỉnh \(I\left( {0;12,5} \right)\) nên ta có \(c = 12,5\).
\(\left( P \right)\) cắt trục hoành tại hai điểm \(A\left( { - 4;0} \right)\) và \(B\left( {4;0} \right)\) nên ta có \(0 = 16a + c \Rightarrow a = \frac{{ - c}}{{16}} = - \frac{{25}}{{32}}\).
Do đó \(\left( P \right):y = - \frac{{25}}{{32}}{x^2} + 12,5\).
Diện tích của cổng là: \(S = \int\limits_{ - 4}^4 {\left( { - \frac{{25}}{{32}}{x^2} + 12,5} \right)dx = \frac{{200}}{3}\left( {{m^2}} \right)} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận