Một nhà máy cần thiết kế một chiếc bể đựng nước hình trụ bằng tôn có nắp, có thể tích là 64π (m³).

Mỗi phát biểu sau đây là đúng hay sai?

Phát biểu	ĐÚNG	SAI
Bán kính đáy của hình trụ là \(\sqrt[3]{{32}}m\) thì bể nước được làm ra tốn ít nguyên liệu nhất.
Nếu giá nguyên liệu \(1{m^2}\) tôn làm bể là 105000 đồng thì chi phí tối thiểu để mua nguyên liệu làm bể nước trên là 18 triệu 949 nghìn đồng (kết quả làm tròn đến nghìn đồng).

Đáp án: “200/3”

Giải thích

Xét hệ trục tọa độ như hình vẽ với trục đối xứng của Parabol trùng với trục tung, trục hoành trùng với đường tiếp đất của cổng.

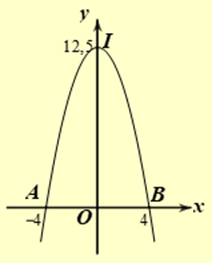
Khi đó Parabol có phương trình dạng \(y = a{x^2} + c\).

Vì \(\left( P \right)\) đi qua đỉnh \(I\left( {0;12,5} \right)\) nên ta có \(c = 12,5\).

\(\left( P \right)\) cắt trục hoành tại hai điểm \(A\left( { - 4;0} \right)\) và \(B\left( {4;0} \right)\) nên ta có \(0 = 16a + c \Rightarrow a = \frac{{ - c}}{{16}} =  - \frac{{25}}{{32}}\).

Do đó \(\left( P \right):y =  - \frac{{25}}{{32}}{x^2} + 12,5\).

Diện tích của cổng là: \(S = \int\limits_{ - 4}^4 {\left( { - \frac{{25}}{{32}}{x^2} + 12,5} \right)dx = \frac{{200}}{3}\left( {{m^2}} \right)} \).