Câu hỏi:
12/11/2024 42
Cho lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Hình chiếu của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trung điểm \(BC\). Cho biết góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'} \right)\) bằng \({60^ \circ }\).
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu
ĐÚNG
SAI
Khoảng cách giữa \(A'B'\) và \(BC\) bằng \(\frac{{3a}}{4}\).
Khoảng cách từ \(A'\) đến \({\rm{mp}}\left( {BCC'B'} \right)\) bằng \(\frac{{3a\sqrt {14} }}{7}\).
Cho lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác đều cạnh \(a\). Hình chiếu của \(A'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trung điểm \(BC\). Cho biết góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'} \right)\) bằng \({60^ \circ }\).
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Khoảng cách giữa \(A'B'\) và \(BC\) bằng \(\frac{{3a}}{4}\). |
||
|
Khoảng cách từ \(A'\) đến \({\rm{mp}}\left( {BCC'B'} \right)\) bằng \(\frac{{3a\sqrt {14} }}{7}\). |
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Khoảng cách giữa \(A'B'\) và \(BC\) bằng \(\frac{{3a}}{4}\). |
X | |
|
Khoảng cách từ \(A'\) đến \({\rm{mp}}\left( {BCC'B'} \right)\) bằng \(\frac{{3a\sqrt {14} }}{7}\). |
X |
Giải thích
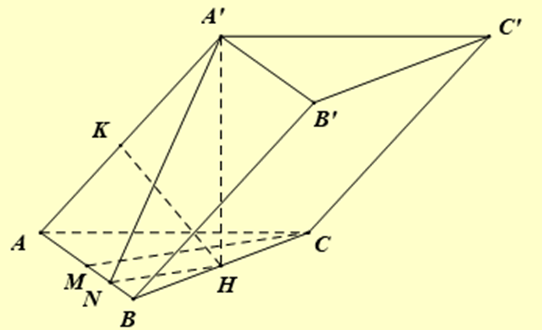
Gọi \(H\) là trung điểm \(BC\), theo giả thiết \(A'H \bot \left( {ABC} \right)\).
Vì là tam giác đều nên \(AH \bot BC\). Vậy \(BC \bot \left( {A'AH} \right) \Rightarrow BC \bot AA'\).
Gọi \(M\) là trung điểm \(AB,N\) là trung điểm \(MB\). Ta có \(CM \bot AB,NH\) là đường trung bình nên \(HN//CM \Rightarrow HN \bot AB\). Mà góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {A'B'C'} \right)\) bằng góc giữa hai mặt phẳng \(\left( {ABB'A'} \right)\) và \(\left( {ABC} \right)\) là góc \(\widehat {A'NH} = {60^ \circ }\).
Ta có \(HN = \frac{1}{2}CM = \frac{{a\sqrt 3 }}{4} \Rightarrow A'H = NH.{\rm{tan}}{60^ \circ } = \frac{{3a}}{4}\).
Vì \(A'H \bot \left( {ABC} \right)\) nên \(A'H \bot BC\), mặt khác \(A'H \bot \left( {A'B'C'} \right)\) nên \(A'H \bot A'B'\)
\( \Rightarrow d\left( {A'B',BC} \right) = A'H = \frac{{3a}}{4}\).
Trong mặt phẳng \(\left( {A'AH} \right)\), kẻ \(HK \bot AA'\) tại \(K\). Ta thấy \(HK \bot AA'\) mà \(AA'//BB' \Rightarrow HK \bot BB'\), \(HK \bot BC\) nên \(HK \bot \left( {BCC'B'} \right)\).
Vì \(AA'//BB'\) nên \(d\left( {A';\left( {BCC'B'} \right)} \right) = d\left( {K;\left( {BCC'B'} \right)} \right) = HK\).
Trong \({\rm{\Delta }}A'AH\) có \(AH = \frac{{a\sqrt 3 }}{2};A'H = \frac{{3a}}{4}\) nên \(\frac{1}{{H{K^2}}} = \frac{1}{{A'{H^2}}} + \frac{1}{{A{H^2}}} = \frac{{16}}{{9{a^2}}} + \frac{4}{{3{a^2}}} = \frac{{28}}{{9{a^2}}}\)
\( \Rightarrow HK = \frac{{3a\sqrt 7 }}{{14}}\).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\) và có đồ thị là đường gấp khúc \(ABC\) như hình vẽ
![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\) và có đồ thị là đường gấp khúc \(ABC\) như hình vẽ Biết \(F\) là nguyên hàm của \(f\) thỏa mãn \(F\left( { - 1} \right) = - 1\). Giá trị của \(F\left( 4 \right) + F\left( 6 \right)\) bằng (1) _______. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid11-1731398057.png)
Biết \(F\) là nguyên hàm của \(f\) thỏa mãn \(F\left( { - 1} \right) = - 1\). Giá trị của \(F\left( 4 \right) + F\left( 6 \right)\) bằng (1) _______.
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\) và có đồ thị là đường gấp khúc \(ABC\) như hình vẽ
Biết \(F\) là nguyên hàm của \(f\) thỏa mãn \(F\left( { - 1} \right) = - 1\). Giá trị của \(F\left( 4 \right) + F\left( 6 \right)\) bằng (1) _______.
Xem đáp án »
12/11/2024
844
Câu 2:
Theo bài viết, mối quan hệ giữa đô thị hóa và những công trình lịch sử chứa đựng nhiều yếu tố văn hóa là sự tác động qua lại, mang đến những giá trị mới cho hình ảnh đô thị là đúng hay sai?
Theo bài viết, mối quan hệ giữa đô thị hóa và những công trình lịch sử chứa đựng nhiều yếu tố văn hóa là sự tác động qua lại, mang đến những giá trị mới cho hình ảnh đô thị là đúng hay sai?
Xem đáp án »
05/07/2024
625
Câu 3:
Phần tư duy đọc hiểu
Đâu KHÔNG phải là hậu quả của việc tắc nghẽn giao thông?
Xem đáp án »
05/07/2024
482
Câu 4:
Kéo thả các từ vào vị trí thích hợp.
quy mô quần thể, tốc độ sinh trưởng, thời gian kiếm ăn, tỉ lệ sinh sản/ tử vong
Theo nhà nghiên cứu 1, yếu tố _______ không thể theo dõi một cách dễ dàng ở loài chim biển.
Kéo thả các từ vào vị trí thích hợp.
quy mô quần thể, tốc độ sinh trưởng, thời gian kiếm ăn, tỉ lệ sinh sản/ tử vong
Theo nhà nghiên cứu 1, yếu tố _______ không thể theo dõi một cách dễ dàng ở loài chim biển.
Xem đáp án »
13/07/2024
436
Câu 5:
Phát biểu sau đúng hay sai?
Dựa trên lời giải thích của học sinh 3, trong các khí được liệt kê ở Bảng 1 thì xenon lan ra nhanh nhất ở 25°C.
Phát biểu sau đúng hay sai?
Dựa trên lời giải thích của học sinh 3, trong các khí được liệt kê ở Bảng 1 thì xenon lan ra nhanh nhất ở 25°C.
Xem đáp án »
05/07/2024
435
Câu 6:
Phần tư duy khoa học / giải quyết vấn đề
Sao Diêm Vương có đường kính xấp xỉ
Xem đáp án »
05/07/2024
391
về câu hỏi!