Câu hỏi:
12/11/2024 365
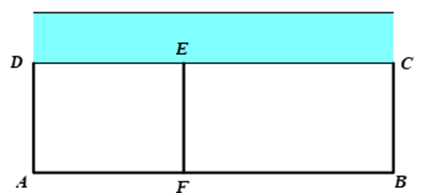
Cho một cái hộp có nắp có dạng hình trụ có bán kính đáy là 10cm và khoảng cách giữa hai đáy là 56cm. Thả các quả bóng có dạng hình cầu vào trong hộp sao cho các quả bóng tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Gọi (P) là mặt phẳng song song với trục và cắt hình trụ theo thiết diện ABCD.
Mỗi phát biểu sau đây là đúng hay sai?
Phát biểu
ĐÚNG
SAI
Thể tích của hộp là \(5600\pi {\rm{c}}{{\rm{m}}^3}\).
Hộp đựng được tối đa 4 quả bóng.
Để diện tích \(ABCD\) bằng \(80{\rm{\;c}}{{\rm{m}}^2}\) thì khoảng cách từ trục đến mặt phẳng \(\left( P \right)\) là \(\frac{{465}}{{49}}{\rm{\;cm}}\).
Cho một cái hộp có nắp có dạng hình trụ có bán kính đáy là 10cm và khoảng cách giữa hai đáy là 56cm. Thả các quả bóng có dạng hình cầu vào trong hộp sao cho các quả bóng tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Gọi (P) là mặt phẳng song song với trục và cắt hình trụ theo thiết diện ABCD.
Mỗi phát biểu sau đây là đúng hay sai?
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích của hộp là \(5600\pi {\rm{c}}{{\rm{m}}^3}\). |
||
|
Hộp đựng được tối đa 4 quả bóng. |
||
|
Để diện tích \(ABCD\) bằng \(80{\rm{\;c}}{{\rm{m}}^2}\) thì khoảng cách từ trục đến mặt phẳng \(\left( P \right)\) là \(\frac{{465}}{{49}}{\rm{\;cm}}\). |
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án
|
Phát biểu |
ĐÚNG |
SAI |
|
Thể tích của hộp là \(5600\pi {\rm{c}}{{\rm{m}}^3}\). |
X | |
|
Hộp đựng được tối đa 4 quả bóng. |
X | |
|
Để diện tích \(ABCD\) bằng \(80{\rm{\;c}}{{\rm{m}}^2}\) thì khoảng cách từ trục đến mặt phẳng \(\left( P \right)\) là \(\frac{{465}}{{49}}{\rm{\;cm}}\). |
X |
Giải thích
Thể tích của hộp là \(V = \pi {R^2}h = \pi {.10^2}.56 = 5600\pi \left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Tổng chiều cao của \(n\) quả bóng thả trong hộp là: \(2nR = 2n.10 = 20n\).
Ta có: \(20n \le 56 \Leftrightarrow n \le 2,8\).
Vậy hộp chỉ đựng được tối đa 2 quả bóng.
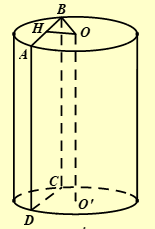
Vì \(\left( P \right)//OO'\) nên \(d\left( {OO';\left( P \right)} \right) = d\left( {O;\left( P \right)} \right) = OH\) (với \(H\) là trung điểm cạnh \(AB\))
Ta có: \({S_{ABCD}} = 80 \Leftrightarrow AB.AD = 80 \Leftrightarrow AB = \frac{{10}}{7}\left( {AD = h = 56} \right)\)
\( \Leftrightarrow 2BH = \frac{{10}}{7} \Leftrightarrow \sqrt {{R^2} - O{H^2}} = \frac{5}{7} \Leftrightarrow OH = \frac{{5\sqrt {149} }}{7}\left( {{\rm{cm}}} \right)\)
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\) và có đồ thị là đường gấp khúc \(ABC\) như hình vẽ Biết \(F\) là nguyên hàm của \(f\) thỏa mãn \(F\left( { - 1} \right) = - 1\). Giá trị của \(F\left( 4 \right) + F\left( 6 \right)\) bằng (1) _______. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid11-1731398057.png)
Lời giải
Đáp án
Biết \(F\) là nguyên hàm của \(f\) thỏa mãn \(F\left( { - 1} \right) = - 1\). Giá trị của \(F\left( 4 \right) + F\left( 6 \right)\) bằng (1) __5__.
Giải thích
Từ đồ thị của hàm số ta xác định được \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}1&{{\rm{\;khi\;}} - 1 \le x < 2}\\{ - \frac{1}{2}x + 2}&{{\rm{\;khi\;}}2 \le x \le 6}\end{array}} \right.\).
Do \(F\) là nguyên hàm của \(f\) nên \(F\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + {C_1}}&{{\rm{\;khi\;}} - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x + {C_2}}&{{\rm{khi\;}}2 \le x \le 6\,\,\,}\end{array}} \right.\).
Ta có \(F\left( { - 1} \right) = - 1 \Leftrightarrow - 1 + {C_1} = - 1 \Leftrightarrow {C_1} = 0\).
Hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right] \Rightarrow F\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\).
\( \Rightarrow F\left( x \right)\) liên tục tại \(x = 2\)
![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;6} \right]\) và có đồ thị là đường gấp khúc \(ABC\) như hình vẽ Biết \(F\) là nguyên hàm của \(f\) thỏa mãn \(F\left( { - 1} \right) = - 1\). Giá trị của \(F\left( 4 \right) + F\left( 6 \right)\) bằng (1) _______. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2024/11/blobid12-1731398079.png)
Suy ra \(F\left( x \right) = \left\{ {\begin{array}{*{20}{c}}x&{{\rm{\;khi\;}} - 1 \le x < 2}\\{ - \frac{1}{4}{x^2} + 2x - 1}&{{\rm{khi\;}}2 \le x \le 6\,\,}\end{array}} \right.\).
Vậy \(F\left( 4 \right) + F\left( 6 \right) = 5\).
Lời giải
Đáp án
Mức cường độ âm thấp nhất mà tai người có thể nghe được là 0 B.
Khi mức cường độ âm đạt đến ngưỡng đau \(\left( {13B} \right)\) thì cường độ âm là 10 \({\rm{W}}/{{\rm{m}}^2}\).
Giải thích
Cường độ âm thấp nhất là \(I = {I_0}\). Khi đó, mức cường độ âm thấp nhất mà tai người có thể nghe được là \(L = {\rm{log}}1 = 0\left( B \right)\).
Khi \(L = 13\left( B \right)\) thì \(I = {10^L}{I_0} = {10^{13}}{.10^{ - 12}} = 10\left( {{\rm{W}}/{{\rm{m}}^2}} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 1)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 24)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 2)
-
Đề thi thử đánh giá tư duy Đại học Bách khoa Hà Nội năm 2024 có đáp án (Đề 18)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 4)
-
Đề thi Đánh giá tư duy Đại học Bách khoa Hà Nội có đáp án (Đề 6)
-
ĐGTD ĐH Bách khoa - Đọc hiểu chủ đề môi trường - Đề 1
-
ĐGTD ĐH Bách khoa - Tư duy Toán học - Xác suất của biến cố và các quy tắc tính xác suất