Giải bài toán sau bằng cách lập hệ phương trình:
Bác Nam mua một thùng trái cây nặng 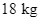 gồm hai loại là táo và xoài. Biết táo có giá
gồm hai loại là táo và xoài. Biết táo có giá 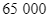 đồng/kg, xoài có giá
đồng/kg, xoài có giá 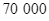 đồng/kg và giá tiền của thùng trái cây là
đồng/kg và giá tiền của thùng trái cây là 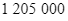 đồng. Hỏi bác mua bao nhiêu kg táo và xoài mỗi loại?
đồng. Hỏi bác mua bao nhiêu kg táo và xoài mỗi loại?
Bác Nam mua một thùng trái cây nặng ![]() gồm hai loại là táo và xoài. Biết táo có giá
gồm hai loại là táo và xoài. Biết táo có giá ![]() đồng/kg, xoài có giá
đồng/kg, xoài có giá ![]() đồng/kg và giá tiền của thùng trái cây là
đồng/kg và giá tiền của thùng trái cây là ![]() đồng. Hỏi bác mua bao nhiêu kg táo và xoài mỗi loại?
đồng. Hỏi bác mua bao nhiêu kg táo và xoài mỗi loại?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Gọi ![]() lần lượt là khối lượng táo, xoài mà bác Nam mua (
lần lượt là khối lượng táo, xoài mà bác Nam mua (![]() đơn vị: kg).
đơn vị: kg).
Theo bài, bác Nam mua một thùng trái cây nặng ![]() kg gồm hai loại là táo và xoài nên ta có phương trình:
kg gồm hai loại là táo và xoài nên ta có phương trình: ![]() (1)
(1)
Số tiền bác Nam dùng để mua táo là: ![]() (nghìn đồng).
(nghìn đồng).
Số tiền bác Nam dùng để mua xoài là: ![]() (nghìn đồng).
(nghìn đồng).
Theo bài, giá tiền của thùng trái cây là ![]() đồng (hay
đồng (hay ![]() nghìn đồng) nên ta có phương trình: nên
nghìn đồng) nên ta có phương trình: nên ![]() (2)
(2)
Từ (1) và (2) ta có hệ phương trình 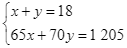
Từ phương trình (1), ta có: ![]() , thế vào phương trình (2), ta được:
, thế vào phương trình (2), ta được:
![]()
![]()
![]()
![]()
![]() (thỏa mãn).
(thỏa mãn).
Thay ![]() vào phương trình
vào phương trình ![]() , ta được:
, ta được: ![]() (thỏa mãn).
(thỏa mãn).
Vậy bác Nam đã mua 11 kg táo và 7 kg xoài.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
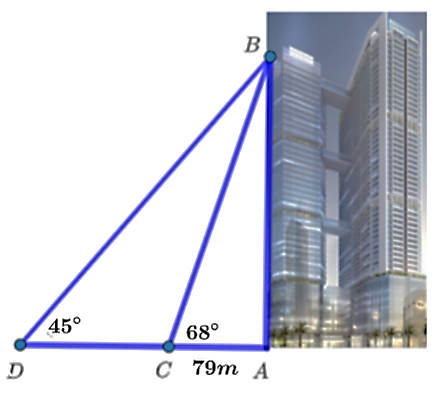
Chiều cao của tòa tháp chính là độ dài đoạn ![]() .
.
Xét tam giác ![]() vuông tại
vuông tại ![]() , ta có:
, ta có: ![]()
Xét tam giác ![]() vuông tại
vuông tại ![]() , ta có:
, ta có: ![]()
Suy ra ![]()
Vận tốc trung bình của chiếc người đó khoảng: ![]()
Vậy vận tốc trung bình của người đó là khoảng ![]() .
.
Lời giải
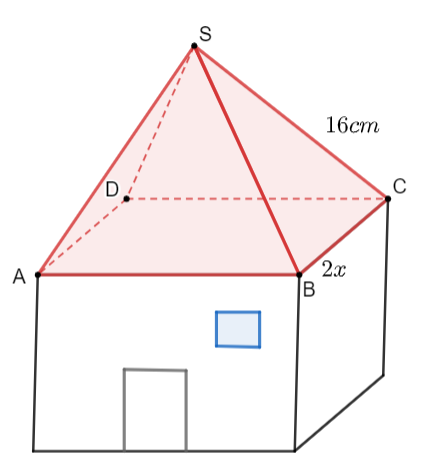
⦁ Diện tích giấy màu cần sử dụng chính bằng tổng diện tích bốn mặt bên là các tam giác cân có cạnh bên bằng 16 cm và cạnh đáy là 2x cm.
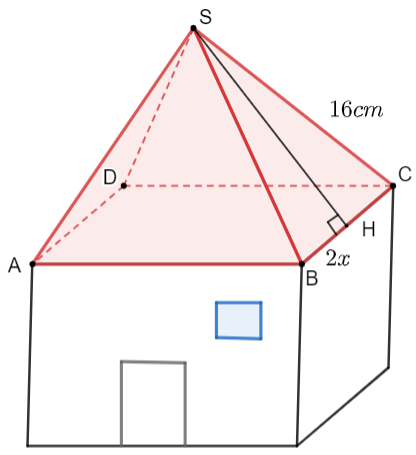
Xét tam giác \(SBC\), kẻ đường cao \(SH \bot BC\) tại \(H\).
Do tam giác \(SBC\) cân tại \(S\) nên \(SH\) vừa là đường cao, vừa là đường trung tuyến của tam giác, suy ra \(H\) là trung điểm của \(BC\).
Suy ra \(BH = HC = \frac{{BC}}{2} = x{\rm{ (cm) }}\left( {0 < x < 16} \right)\).
Áp dụng định lí Pythagore vào tam giác \(SHC\) vuông tại \(H\), ta có: \(S{H^2} + H{C^2} = S{C^2}\)
Suy ra \(S{H^2} = {16^2} - {x^2} = 256 - {x^2}.\)
Do đó \(SH = \sqrt {256 - {x^2}} {\rm{\;(cm)}}{\rm{.}}\)
Diện tích tam giác \(SBC\) là \(\frac{1}{2}SH \cdot BC = \frac{1}{2} \cdot \sqrt {256 - {x^2}} \cdot 2x = x\sqrt {256 - {x^2}} {\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Diện tích giấy màu cần sử dụng là \(S = 4x\sqrt {256 - {x^2}} {\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
⦁ Yêu cầu bài toán đưa về thực hiện tìm giá trị lớn nhất của \(S = 4x\sqrt {256 - {x^2}} {\rm{ }}\)với \(0 < x < 16\).
Ta có: \(4x\sqrt {256 - {x^2}} = 4\sqrt {256{x^2} - {x^4}} \)
\( = 4\sqrt { - \left( {{x^4} - 2 \cdot 128{x^2} + {{128}^2}} \right) + {{128}^2}} \)
\( = 4\sqrt { - {{\left( {{x^2} - 128} \right)}^2} + {{128}^2}} \le 4\sqrt {{{128}^2}} = 512\)
Do đó, \(S \le 512\).
Dấu “=” xảy ra khi và chỉ khi \({x^2} - 128 = 0\) hay \(x = 8\sqrt 2 \) (do \(0 < x < 16)\).
Khi đó, độ dài cạnh đáy của phần mái là \(16\sqrt 2 {\rm{ cm}}.\)
Vậy diện tích giấy màu cần sử dụng nhiều nhất là \(512{\rm{ c}}{{\rm{m}}^2}\) khi độ dài cạnh đáy của phần mái là \(16\sqrt 2 {\rm{ cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.