Cho điểm 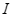 bên trong đường tròn tâm
bên trong đường tròn tâm 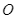 . Cho hai dây cung
. Cho hai dây cung 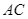 và
và 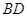 cùng đi qua
cùng đi qua 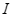 sao cho
sao cho 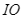 là tia phân giác của
là tia phân giác của 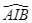 . Vẽ
. Vẽ 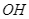 vuông góc với
vuông góc với 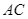 ở
ở 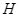 ,
, 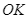 vuông góc với
vuông góc với 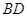 ở
ở 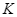 . Chứng minh rằng:
. Chứng minh rằng:
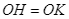 và
và 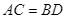 .
.
Cho điểm ![]() bên trong đường tròn tâm
bên trong đường tròn tâm ![]() . Cho hai dây cung
. Cho hai dây cung ![]() và
và ![]() cùng đi qua
cùng đi qua ![]() sao cho
sao cho ![]() là tia phân giác của
là tia phân giác của ![]() . Vẽ
. Vẽ ![]() vuông góc với
vuông góc với ![]() ở
ở ![]() ,
, ![]() vuông góc với
vuông góc với ![]() ở
ở ![]() . Chứng minh rằng:
. Chứng minh rằng:
![]() và
và ![]() .
.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:

⦁ Xét ![]() và
và ![]() có:
có:
![]() ,
, ![]() là cạnh chung và
là cạnh chung và ![]() (do
(do ![]() là tia phân giác của
là tia phân giác của ![]() .
.
Do đó ![]() (cạnh huyền – góc nhọn).
(cạnh huyền – góc nhọn).
Suy ra ![]() (hai cạnh tương ứng).
(hai cạnh tương ứng).
⦁ Xét ![]() và
và ![]() có:
có:
![]() ,
, ![]() ,
, ![]()
Do đó ![]() (cạnh huyền – cạnh góc vuông).
(cạnh huyền – cạnh góc vuông).
Suy ra ![]() (hai cạnh tương ứng).
(hai cạnh tương ứng).
Xét ![]() cân tại
cân tại ![]() (do
(do ![]() cùng là bán kính đường tròn tâm
cùng là bán kính đường tròn tâm ![]() nên đường cao
nên đường cao ![]() đồng thời là đường trung tuyến của tam giác, do đó
đồng thời là đường trung tuyến của tam giác, do đó ![]() là trung điểm của
là trung điểm của ![]() Suy ra
Suy ra ![]()
Chứng minh tương tự, ta có ![]() là trung điểm của
là trung điểm của ![]() Suy ra
Suy ra ![]()
Do đó ![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
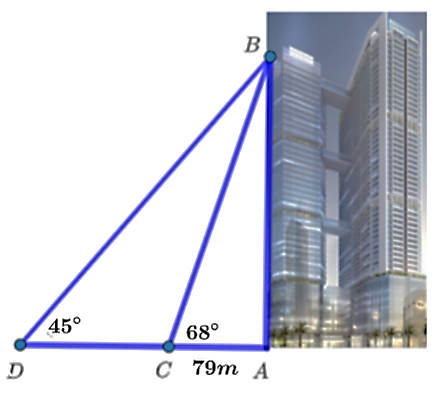
Chiều cao của tòa tháp chính là độ dài đoạn ![]() .
.
Xét tam giác ![]() vuông tại
vuông tại ![]() , ta có:
, ta có: ![]()
Xét tam giác ![]() vuông tại
vuông tại ![]() , ta có:
, ta có: ![]()
Suy ra ![]()
Vận tốc trung bình của chiếc người đó khoảng: ![]()
Vậy vận tốc trung bình của người đó là khoảng ![]() .
.
Lời giải
Gọi ![]() lần lượt là khối lượng táo, xoài mà bác Nam mua (
lần lượt là khối lượng táo, xoài mà bác Nam mua (![]() đơn vị: kg).
đơn vị: kg).
Theo bài, bác Nam mua một thùng trái cây nặng ![]() kg gồm hai loại là táo và xoài nên ta có phương trình:
kg gồm hai loại là táo và xoài nên ta có phương trình: ![]() (1)
(1)
Số tiền bác Nam dùng để mua táo là: ![]() (nghìn đồng).
(nghìn đồng).
Số tiền bác Nam dùng để mua xoài là: ![]() (nghìn đồng).
(nghìn đồng).
Theo bài, giá tiền của thùng trái cây là ![]() đồng (hay
đồng (hay ![]() nghìn đồng) nên ta có phương trình: nên
nghìn đồng) nên ta có phương trình: nên ![]() (2)
(2)
Từ (1) và (2) ta có hệ phương trình 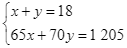
Từ phương trình (1), ta có: ![]() , thế vào phương trình (2), ta được:
, thế vào phương trình (2), ta được:
![]()
![]()
![]()
![]()
![]() (thỏa mãn).
(thỏa mãn).
Thay ![]() vào phương trình
vào phương trình ![]() , ta được:
, ta được: ![]() (thỏa mãn).
(thỏa mãn).
Vậy bác Nam đã mua 11 kg táo và 7 kg xoài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.