Cho hai tiếp tuyến 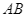 và
và 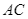 của đường tròn tâm
của đường tròn tâm 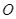 (
(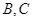 là hai tiếp điểm). Vẽ đường kính
là hai tiếp điểm). Vẽ đường kính 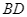 ,
, 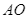 cắt
cắt 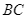 tại
tại 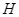 .
Chứng minh
.
Chứng minh 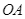 vuông góc với
vuông góc với 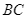 và
và 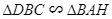 .
.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
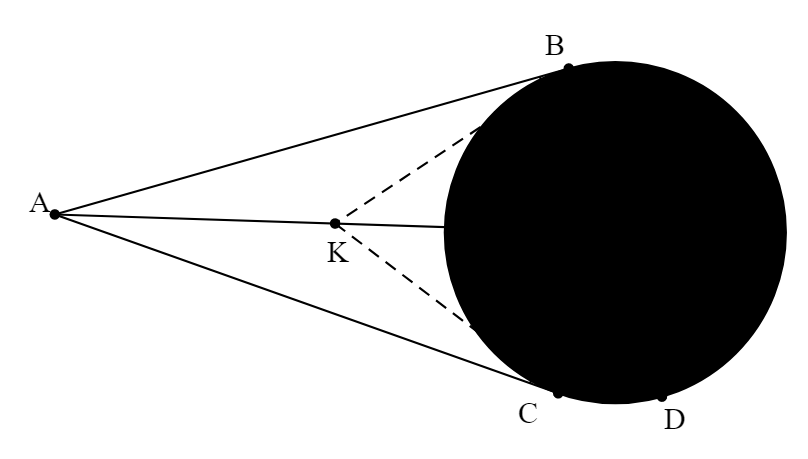
⦁ Theo tính chất hai tiếp tuyến cắt nhau tại ![]() của đường tròn
của đường tròn ![]() ta có:
ta có: ![]() suy ra
suy ra ![]() thuộc đường trung trực của
thuộc đường trung trực của ![]() (3).
(3).
Lại có ![]() suy ra
suy ra ![]() thuộc đường trung trực của
thuộc đường trung trực của ![]() (4).
(4).
Từ (3) và (4) suy ra ![]() là đường trung trực của
là đường trung trực của ![]() hay
hay ![]() vuông góc với
vuông góc với ![]() tại
tại ![]() .
.
⦁ Xét đường tròn ![]() đường kính
đường kính ![]() có
có ![]() là góc nội tiếp chắn nửa đường tròn nên
là góc nội tiếp chắn nửa đường tròn nên ![]()
Ta có: ![]() (tổng hai góc nhọn của tam giác
(tổng hai góc nhọn của tam giác ![]() vuông tại
vuông tại ![]() và
và ![]()
Suy ra ![]() .
.
Xét ![]() và
và ![]() có:
có: ![]() và
và ![]()
Do đó ![]() (g.g).
(g.g).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
Bán kính của đường tròn lớn là: ![]()
Bán kính của đường tròn nhỏ là: ![]()
Diện tích bề mặt trên chiếc đèn chính là diện tích hình vành khuyên được giới hạn bởi hai đường tròn có bán kính lần lượt là ![]() và bằng:
và bằng:
![]()
Lời giải
Gọi \[x,y\] lần lượt là giá niêm yết của loại vé I và II (\[x,y > 0\], đơn vị: nghìn đồng).
• Tuần lễ kích cầu du lịch:
Giá loại vé I giảm 15%, tức là sẽ có giá 100% – 15% = 85% của giá niêm yết nên giá bán vé loại I lúc này là \[85\% x = 0,85x\] (nghìn đồng).
Giá loại vé II giảm 10%, tức là sẽ có giá 100% – 10% = 90% của giá niêm yết nên giá bán vé loại II lúc này là \[90\% y = 0,9y\] (nghìn đồng).
Do đó, tổng số tiền khi anh Bảo mua 3 vé loại I và 2 vé loại II là:
\[3 \cdot 0,85x + 2 \cdot 0,9y = 2,55x + 1,8y\] (nghìn đồng).
Theo bài, anh Bảo phải trả số tiền là \(24\,\,825\,\,000\) đồng (hay \(24\,\,825\) nghìn đồng) nên ta có phương trình:
\[2,55x + 1,8y = 24\,\,825\] hay \[0,85x + 0,6y = 8\,\,275\] (1)
• Tuần lễ Quốc tế Lao động:
Giá loại vé I giảm 10%, tức là sẽ có giá 100% – 10% = 90% của giá niêm yết nên giá bán vé loại I lúc này là \[90\% x = 0,9x\] (nghìn đồng).
Giá loại vé II giảm 15%, tức là sẽ có giá 100% – 15% = 85% của giá niêm yết nên giá bán vé loại II lúc này là \[85\% y = 0,85y\] (nghìn đồng).
Do đó, tổng số tiền khi anh Bình mua 3 vé loại I và 4 vé loại II là:
\[3 \cdot 0,9x + 4 \cdot 0,85y = 2,7x + 3,4y\] (nghìn đồng).
Theo bài, anh Bình phải trả số tiền là \(37\,\,790\,\,000\) đồng (hay \(37\,\,790\)nghìn đồng) nên ta có phương trình:
\[2,7x + 3,4y = 37\,\,790\] (2)
Từ (1) và (2) ta có hệ phương trình: \[\left\{ \begin{array}{l}0,85x + 0,6y = 8\,\,275\\2,7x + 3,4y = 37\,\,790.\end{array} \right.\]
Nhân cả hai vế của phương trình (1) với 1,7 và nhân cả hai vế của phương trình (2) với 0,3, ta được hệ phương trình mới là: \[\left\{ \begin{array}{l}1,445x + 1,02y = 14\,\,067,5\\0,81x + 1,02y = 11\,\,337.\end{array} \right.\]
Trừ từng vế của phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:
\[0,635x = 2730,5\] suy ra \[x = 4300\] (thỏa mãn).
Thay \[x = 4\,\,300\] vào phương trình (1), ta được:
\[2,55 \cdot 4\,\,300 + 1,8y = 24\,\,825\] suy ra \(1,8y = 13\,\,860\) nên \[y = 7\,\,700\] (thỏa mãn).
Ta có \[4\,\,300\] nghìn đồng tức là \[4{\rm{ 300 000}}\] đồng; \[7\,\,700\] nghìn đồng là \[7{\rm{ }}700{\rm{ 000}}\] đồng.
Vậy giá niêm yết của loại vé I là \[4{\rm{ 300 000}}\] đồng và giá niêm yết của loại vé II là \[7{\rm{ }}700{\rm{ 000}}\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.