Câu hỏi:
11/12/2024 288
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
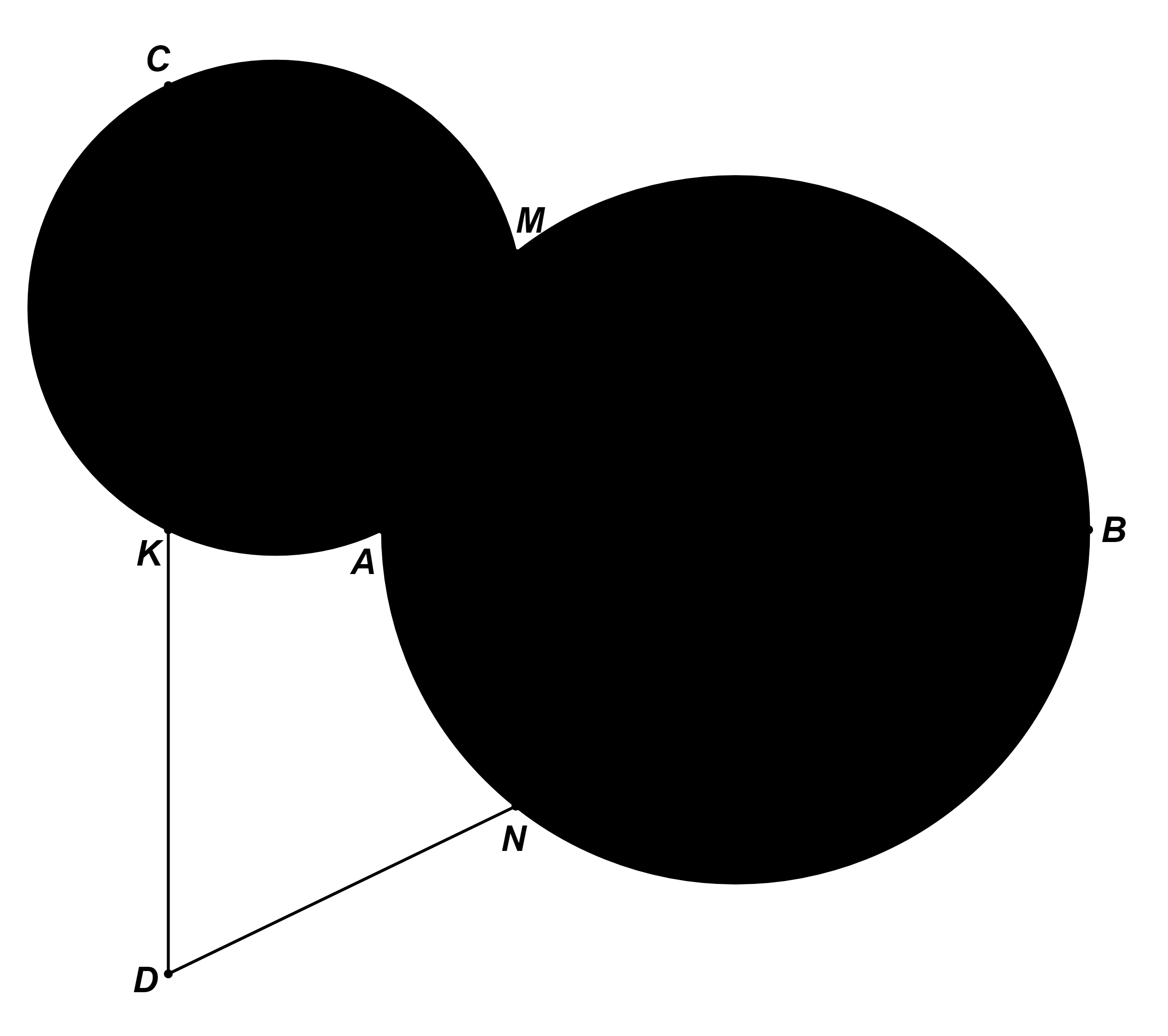
⦁ Xét 
có 
vừa là đường cao, vừa là đường phân giác của nên cân tại 
Do đó 
. (1)
Ta có: 
(cùng phụ với 
) (2)
Xét đường tròn 
có 
(góc nội tiếp cùng chắn cung 
) (3)
Từ (1), (2) và (3) suy ra 
Xét 
có 
nên cân tại 
.
⦁ Xét 
cân tại 
(do 
) ta có 
.
Mà 
(do là đường phân giác của 
).
Suy ra 
Xét 
vuông tại 
ta có: 
Mà 
và 
nên 
Do đó, 
.
Suy ra 
tại 
thuộc đường tròn 
.
Vậy 
là tiếp tuyến của đường tròn .
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
Diện tích lối đi của công viên là: 
Lời giải
Gọi 
lần lượt là giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu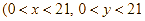 
, triệu đồng).
Theo đề, giá niêm yết của một chiếc bếp từ đôi và một chiếc nồi chiên không dầu tổng cộng là 
triệu đồng nên ta có phương trình: 
. (1)
Bếp từ đôi giảm giá 
, tức là có giá bằng 
giá niêm yết , nghĩa là giá của một bếp từ đôi sau khi giảm là 
.
Nồi chiên không dầu giảm giá 
, tức là có giá bằng 
giá niêm yết, nghĩa là giá của một nồi chiên không dầu sau khi giảm là 
.
Bác Lan mua hai sản phẩm sau khi giảm giá với số tiền 
triệu đồng nên ta có phương trình:
. (2)
Từ (1) và (2) ta có hệ phương trình: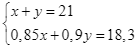 
.
Từ phương trình thứ nhất, ta có: 
, thế vào phương trình thứ hai, ta được:
(thỏa mãn).
Thay vào phương trình (*), ta được 
(thỏa mãn).
Vậy giá niêm yết của bếp từ đôi và nồi chiên không dầu lần lượt là 
triệu đồng và 
triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1