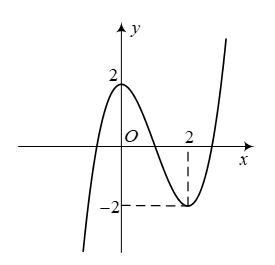
Trong không gian tọa độ \(Oxyz\), gọi \(A,B,C\) lần lượt là hình chiếu của \[M\left( {3;3;3} \right)\] lên các trục tọa độ \(Ox,Oy,Oz\). Giả sử \[H\left( {a;b;c} \right)\] là trực tâm tam giác \(ABC\). Tính \[{a^2} + {b^2} + {c^2}\].
Trong không gian tọa độ \(Oxyz\), gọi \(A,B,C\) lần lượt là hình chiếu của \[M\left( {3;3;3} \right)\] lên các trục tọa độ \(Ox,Oy,Oz\). Giả sử \[H\left( {a;b;c} \right)\] là trực tâm tam giác \(ABC\). Tính \[{a^2} + {b^2} + {c^2}\].
Quảng cáo
Trả lời:
Ta có: \(M\left( {3;3;3} \right)\), gọi \(A,B,C\) lần lượt là hình chiếu của \(M\) lên các trục tọa độ \(Ox,Oy,Oz\).
\( \Rightarrow A\left( {3;0;0} \right),\,\,B\left( {0;3;0} \right),\,\,\,C\left( {0;0;3} \right)\).
\( \Rightarrow AB = BC = CA = 3\sqrt 2 \).
\( \Rightarrow \Delta ABC\) là tam giác đều.
\( \Rightarrow \) Trực tâm \(H\) trùng với trọng tâm \(G\) của \(\Delta ABC\).
\( \Rightarrow H \equiv G\left( {1;1;1} \right)\).
\[ \Rightarrow {a^2} + {b^2} + {c^2} = 3\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(h\left( t \right) = 2\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 5\)\( \Rightarrow h'\left( t \right) = - \frac{\pi }{6}\sin \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right)\).
\(h'\left( t \right) = 0 \Leftrightarrow \sin \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) = 0 \Leftrightarrow \frac{{\pi t}}{{12}} + \frac{\pi }{3} = k\pi \)\( \Leftrightarrow t = - 4 + 12k\,\,\left( {k \in \mathbb{Z}} \right)\).
Mà \(0 \le t \le 24\) nên \(0 \le - 4 + 12k \le 24 \Leftrightarrow \frac{1}{3} \le k \le \frac{7}{3}\)\( \Rightarrow k \in \left\{ {1\,;\,2} \right\}\).
Do đó \(h'\left( t \right) = 0 \Rightarrow \left[ \begin{array}{l}t = 8\\t = 20\end{array} \right.\).
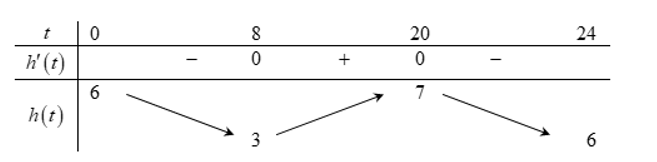
\( \Rightarrow h\left( t \right)\) đồng biến trên khoảng \(\left( {8\,;\,20} \right)\) hay trong khoảng từ \(8\,{\rm{h}}\) đến \(20\,{\rm{h}}\)độ sâu của mực nước trong kênh tăng dần.
Vậy \(a = 8\,;\,b = 20\) và \(a + b = 28\).
Lời giải
Gọi hai kích thước của hình chữ nhật là \(x\) và \(y\), với \(2x + y = 240\) \(\left( {0 < x < 120;0 < y < 240} \right)\).
Suy ra \(y = 240 - 2x\)
Diện tích của mảnh vườn hình chữ nhật là:
\(S = xy = x\left( {240 - 2x} \right) = 240x - 2{x^2},0 < x < 120\).
\(S' = 240 - 4x\); \(S' = 0 \Leftrightarrow x = 60 \in \left( {0;120} \right)\).
Bảng biến thiên
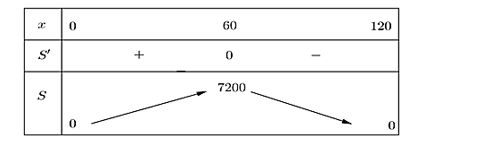
Từ bảng biến thiên ta thấy \(\mathop {\max }\limits_{\left( {0;120} \right)} S = 7200 \Leftrightarrow x = 60\).
Vậy ông nông dân có thể rào được cánh đồng với diện tích lớn nhất là \(7200\)m2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.