Cho hàm số \(y = \frac{{2{x^2} - 2x + 2}}{{ - x + 1}}\) có đồ thị \(\left( C \right)\).
a) Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) ∪ \(\left( {2; + \infty } \right)\).
b) Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {\frac{3}{2};\frac{5}{2}} \right]\) bằng \( - \frac{{19}}{3}\).
c) Đồ thị hàm số \(\left( C \right)\) có tiệm cận xiên là đường thẳng \(2x + y = 0\).
d) Góc giữa hai đường tiệm cận của đồ thị hàm số bằng \(45^\circ \).
Cho hàm số \(y = \frac{{2{x^2} - 2x + 2}}{{ - x + 1}}\) có đồ thị \(\left( C \right)\).
a) Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) ∪ \(\left( {2; + \infty } \right)\).
b) Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {\frac{3}{2};\frac{5}{2}} \right]\) bằng \( - \frac{{19}}{3}\).
c) Đồ thị hàm số \(\left( C \right)\) có tiệm cận xiên là đường thẳng \(2x + y = 0\).
d) Góc giữa hai đường tiệm cận của đồ thị hàm số bằng \(45^\circ \).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) S, b) S, c) Đ, d) S
a) Ta có \(y' = \frac{{ - 2{x^2} + 4x}}{{{{\left( { - x + 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\) và có bảng biến thiên như sau
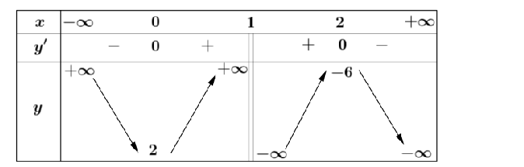
Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
b) Ta có \(y\left( {\frac{3}{2}} \right) = - 7;y\left( 2 \right) = - 6;y\left( {\frac{5}{2}} \right) = - \frac{{19}}{3}\).
Giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {\frac{3}{2};\frac{5}{2}} \right]\) bằng \( - 7\) đạt tại \(x = \frac{3}{2}\).
c) Ta có \(2x + y = 0\)\( \Rightarrow y = - 2x\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{2{x^2} - 2x + 2}}{{ - x + 1}} - \left( { - 2x} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{ - x + 1}} = 0\) nên đồ thị có tiệm cận xiên là đường thẳng \(2x + y = 0\) hay \(y = - 2x\).
d) Ta có \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{2{x^2} - 2x + 2}}{{ - x + 1}} = + \infty \); \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{2{x^2} - 2x + 2}}{{ - x + 1}} = - \infty \) nên \(x = 1\) là tiệm cận đứng của đồ thị hàm số.
Ta có \({d_1}:x - 1 = 0 \Rightarrow \overrightarrow {{n_1}} = \left( {1;0} \right)\); \({d_2}:2x + y = 0\)\( \Rightarrow \overrightarrow {{n_2}} = \left( {2;1} \right)\).
Ta có \(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.2 + 0.1} \right|}}{{\sqrt {{1^2} + {0^2}} .\sqrt {{2^2} + {1^2}} }} = \frac{2}{{\sqrt 5 }}\)\( \Rightarrow \left( {{d_1},{d_2}} \right) \approx 26^\circ 33'\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Vị trí của máy bay sau 5 phút tiếp theo là \(C(x;y;z)\).
Vì hướng của máy bay không đổi nên \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng hướng.
Do vận tốc của máy bay không đổi và thời gian bay từ \(A\) đến \(B\) gấp đôi thời gian bay từ \(B\) đến \(C\) nên \(AB = 2BC\).
Do đó \(\overrightarrow {BC} = \frac{1}{2}\overrightarrow {AB} = \left( {\frac{{940 - 800}}{2};\frac{{550 - 500}}{2};\frac{{9 - 7}}{2}} \right) = \left( {70;25;1} \right)\).
Mặt khác, \(\overrightarrow {BC} = (x - 940;y - 550;z - 9)\) nên \(\left\{ {\begin{array}{*{20}{l}}{x - 940 = 70}\\{y - 550 = 25}\\{z - 9 = 1}\end{array}} \right.\)
Từ đó \(\left\{ {\begin{array}{*{20}{l}}{x = 1010}\\{y = 575}\\{z = 10}\end{array}} \right. \Rightarrow x + y + z = 1595\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) S, b) S, c) Đ, d) S
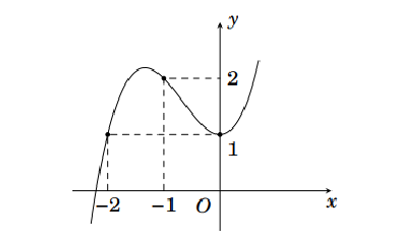
a) Dựa vào đồ thị ta thấy hàm số đồng biến trên khoảng \(\left( { - \infty ;{x_0}} \right)\) với \( - 2 < {x_0} < - 1\).
b) Hàm số đạt cực tiểu tại \(x = 0,{y_{CT}} = 1\).
c) Đồ thị hàm số cắt trục Oy tại điểm có tọa độ \(\left( {0;1} \right)\).
d) Đồ thị đi qua ba điểm \(\left( { - 2;1} \right),\left( { - 1;2} \right),\left( {0;1} \right)\) và đạt cực trị tại \(x = 1\) nên ta có hệ:
\(\left\{ \begin{array}{l} - 8a + 4b - 2c + d = 1\\ - a + b - c + d = 2\\d = 1\\c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 0\\d = 1\end{array} \right. \Rightarrow 2a + 3b + c = 8\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
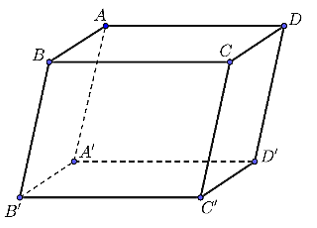
Câu 4
A. \(2\overrightarrow {AA'} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập