Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 10 m, chiều rộng là 6m và chiều cao là 4 m. Một chiếc quạt được treo trên trần nhà sao cho là điểm chính giữa của phòng học.
Xét hệ trục tọa độ \(Oxyz\)có gốc (\(O \equiv A\)) trùng với một góc phòng và mặt phẳng (\(Oxy\)) trùng với mặt sàn, đơn vị đo được lấy theo mét . Gọi \[I(a;b;c)\]là tọa độ của điểm treo quạt. Tính giá trị \(a + b + c\)?
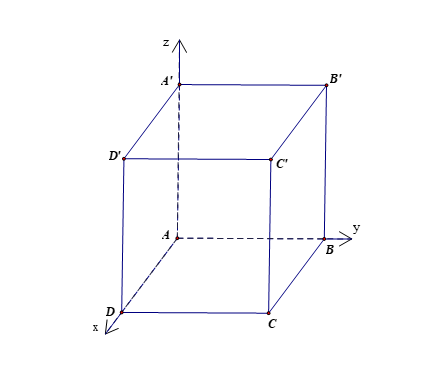
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 10 m, chiều rộng là 6m và chiều cao là 4 m. Một chiếc quạt được treo trên trần nhà sao cho là điểm chính giữa của phòng học.
Xét hệ trục tọa độ \(Oxyz\)có gốc (\(O \equiv A\)) trùng với một góc phòng và mặt phẳng (\(Oxy\)) trùng với mặt sàn, đơn vị đo được lấy theo mét . Gọi \[I(a;b;c)\]là tọa độ của điểm treo quạt. Tính giá trị \(a + b + c\)?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(C'(6;10;4)\), \(A'(0;0;4)\).
Gọi \(I\left( {x;y;z} \right)\) là trung điểm của \(A'C'\).
Do đó \(\left\{ \begin{array}{l}{x_I} = \frac{{6 + 0}}{2} = 3\\{y_I} = \frac{{10 + 0}}{2} = 5\\{z_I} = \frac{{4 + 4}}{2} = 4\end{array} \right.\).
Vậy tọa độ của điểm treo quạt \(I(3;5;4)\)suy ra \(a + b + c = 12\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đ, b) S, c) S, d) S
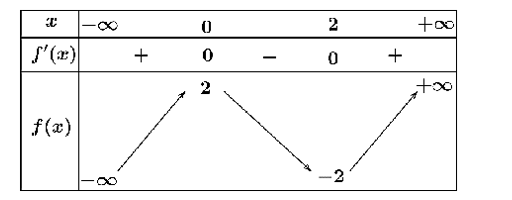
a) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).
b) Ta có \(g'\left( x \right) = 2 - 3f'\left( x \right) > 0,\forall x \in \left( {0;2} \right)\), suy ra hàm số \(g\left( x \right) = 2x - 3f\left( x \right)\) đồng biến trên khoảng \(\left( {0;2} \right)\).
c) Ta có hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
Mà \(0 \le {\sin ^2}x \le 1,\forall x \in \mathbb{R}\)\( \Rightarrow 0 \le {\sin ^2}x < \frac{3}{2},\forall x \in \mathbb{R}\) \( \Rightarrow f\left( {{{\sin }^2}x} \right) > f\left( {\frac{3}{2}} \right)\).
d) Ta có \(y' = {\left( {2 - 3x} \right)^\prime } \cdot f'\left( {2 - 3x} \right) = - 3f'\left( {2 - 3x} \right)\).
Hàm số \(y = f\left( {2 - 3x} \right)\) nghịch biến \(y' = - 3f'\left( {2 - 3x} \right) < 0 \Leftrightarrow f'\left( {2 - 3x} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}2 - 3x < 0\\2 - 3x > 2\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x > \frac{2}{3}\\x < 0\end{array} \right.\). Suy ra hàm số \(y = f\left( {2 - 3x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {\frac{2}{3}; + \infty } \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có \(M \in \left( C \right)\) \( \Rightarrow M\left( {{x_0};{x_0} + \frac{1}{{{x_0} + 1}}} \right)\) với \({x_0} > - 1\).
Ta có \(I{M^2} = {\left( {{x_0} + 1} \right)^2} + {\left( {{x_0} + 1 + \frac{1}{{{x_0} + 1}}} \right)^2} = 2{\left( {{x_0} + 1} \right)^2} + \frac{1}{{{{\left( {{x_0} + 1} \right)}^2}}} + 2\).
Đặt \(t = {\left( {{x_0} + 1} \right)^2},t > 0\) thì khi đó \(I{M^2} = 2t + 2 + \frac{1}{t}\).
Xét hàm số \(y = 2t + 2 + \frac{1}{t}\) có \(y' = 2 - \frac{1}{{{t^2}}} = 0 \Leftrightarrow t = \frac{1}{{\sqrt 2 }}\).
Bảng biến thiên
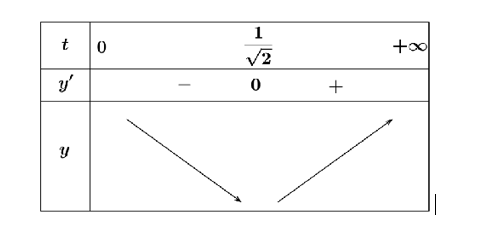
Để thuyền thu được sóng tốt nhất \( \Leftrightarrow IM\) ngắn nhất \( \Leftrightarrow {x_0} = \frac{1}{{\sqrt[4]{2}}} - 1\).
Vậy \(n = 4;a = 2;b = 1 \Rightarrow a \cdot n + b = 9\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right) \cup \left( {1\,;\,3} \right)\).
B. Hàm số nghịch biến trên khoảng \(\left( { - 1;\,3} \right){\rm{\backslash }}\left\{ 1 \right\}\).
C. Hàm số nghịch biến trên mỗi khoảng \(\left( { - 1;\,1} \right)\)và \(\left( {1\,;\,3} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập