Câu hỏi:
14/12/2024 993
Ông An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30 m và chiều dài 50 m. Để giảm bởi chi phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô đen và không tô đen) như hình vẽ. Phần tô đen gồm hai phần diện tích bằng nhau và đường cong \(AIB\) là một parabol đỉnh I được trồng cỏ nhân tạo với giá 130000 đồng/m2 và phần còn lại được trồng với giá 90000 đồng/m2. Hỏi ông An phải trả bao nhiêu tiền (triệu đồng) để trồng cỏ nhân tạo cho sân bóng đá.
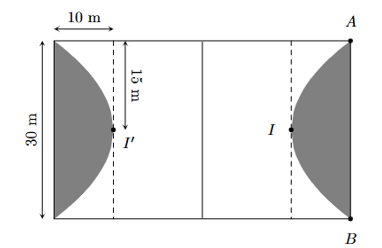
Ông An xây dựng một sân bóng đá mini hình chữ nhật có chiều rộng 30 m và chiều dài 50 m. Để giảm bởi chi phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô đen và không tô đen) như hình vẽ. Phần tô đen gồm hai phần diện tích bằng nhau và đường cong \(AIB\) là một parabol đỉnh I được trồng cỏ nhân tạo với giá 130000 đồng/m2 và phần còn lại được trồng với giá 90000 đồng/m2. Hỏi ông An phải trả bao nhiêu tiền (triệu đồng) để trồng cỏ nhân tạo cho sân bóng đá.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn hệ trục tọa độ sao O là trung điểm của \(AB\), \(I \in Oy\) và \(I\left( {0;10} \right),A\left( { - 15;0} \right),B\left( {15;0} \right)\).
Giả sử \(\left( P \right):y = a{x^2} + bx + c\).
Có \(\left( P \right)\) đi qua \(I\left( {0;10} \right),A\left( { - 15;0} \right),B\left( {15;0} \right)\) nên ta có hệ
\(\left\{ \begin{array}{l}225a + 15b + c = 0\\225a - 15b + c = 0\\c = 10\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{2}{{45}}\\b = 0\\c = 10\end{array} \right.\). Do đó \(\left( P \right):y = \frac{{ - 2}}{{45}}{x^2} + 10\).
Do đó diện tích phần tô đen là \({S_1} = 2\int\limits_{ - 15}^{15} {\left( { - \frac{2}{{45}}{x^2} + 10} \right)dx} = 400\) m2.
Diện tích phần không tô đen là \({S_2} = 30.50 - {S_1} = 1100\) m2.
Số tiền ông An phải trả là: \(400.130000 + 1100.90000 = 151000000\) đồng = 151 triệu đồng.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) S, b) Đ, c) S, d) S
a) Ta có \(v\left( t \right) = \int {a\left( t \right)dt} = \int {\left( {2t - 7} \right)dt} = {t^2} - 7t + C\).
Vì \(v\left( 0 \right) = 6 \Rightarrow C = 6\). Do đó \(v\left( t \right) = {t^2} - 7t + 6\).
b) \(v\left( 7 \right) = {7^2} - 7.7 + 6 = 6\left( {{\rm{m/s}}} \right)\).
c) Có \(s = \int\limits_1^7 {v\left( t \right)dt} = \int\limits_1^7 {\left( {{t^2} - 7t + 6} \right)dt} = \left. {\left( {\frac{{{t^3}}}{3} - \frac{{7{t^2}}}{2} + 6t} \right)} \right|_1^7 = - 18\).
d) Tọa độ của chất điểm tại thời điểm \(t\) là \(x\left( t \right) = \int {v\left( t \right)dt} = \int {\left( {{t^2} - 7t + 6} \right)dt} = \frac{{{t^3}}}{3} - \frac{{7{t^2}}}{2} + 6t + C\)
Ta cần tìm giá trị lớn nhất của \(x\left( t \right)\) với \(t \in \left[ {0;8} \right]\).
Ta có \(x'\left( t \right) = v\left( t \right) = 0\) khi \(t = 1\) hoặc \(t = 6\).
Lại có \(x\left( 0 \right) = C,x\left( 1 \right) = \frac{{17}}{6} + C,x\left( 6 \right) = - 18 + C,x\left( 8 \right) = - \frac{{16}}{3} + C\).
Vậy giá trị lớn nhất của \(x\left( t \right)\) với \(t \in \left[ {0;8} \right]\) đạt được khi \(t = 1\).
Lời giải
Ta có vectơ pháp tuyến của \[\left( \beta \right),\left( P \right),\left( Q \right)\] lần lượt là \[\overrightarrow {{n_1}} \left( {1;2;3} \right),\,\overrightarrow {{n_2}} \left( {1;3;1} \right),\,\overrightarrow {{n_3}} \left( {1; - 1;1} \right)\].
Khi đó \[\overrightarrow {{n_\alpha }} = \left[ {\overrightarrow {{n_1}} ,\left[ {\overrightarrow {{n_2}} ,\overrightarrow {{n_3}} } \right]} \right] = \left( { - 8;16; - 8} \right) = - 8\left( {1; - 2;1} \right)\].
Gọi \[A\left( {x;y;z} \right) \in d\] là giao tuyến của \[\left( P \right)\] và \[\left( Q \right)\], khi đó toạ độ điểm \[A\] thoả mãn hệ \[\left\{ \begin{array}{l}x + 3y + z - 7 = 0\\x - y + z + 1 = 0\end{array} \right.\]. Cho \[x = 0\] ta có \[\left\{ \begin{array}{l}3y + z - 7 = 0\\ - y + z + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\z = 1\end{array} \right.\], khi đó \[A\left( {0;2;1} \right)\].
Do \[\left( \alpha \right)\] chứa giao tuyến của \[\left( P \right)\] và \[\left( Q \right)\] nên \[\left( \alpha \right)\] đi qua \[A\left( {0;2;1} \right)\].
Phương trình \[\left( \alpha \right):x - 2\left( {y - 2} \right) + z - 1 = 0 \Leftrightarrow x - 2y + z + 3 = 0\]. Vậy \[d = 3\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận