PHẦN II. TỰ LUẬN
Trong một phòng thí nghiệm, người ta nuôi một loại vi khuẩn. Lúc đầu có 300 vi khuẩn. Sau một giờ, số vi khuẩn là 705 con. Giả sử số vi khuẩn tăng lên theo công thức tăng trưởng mũ, số vi khuẩn sau \(x\) giờ là \(f\left( x \right) = C.{e^{kx}}\). Tính số lượng vi khuẩn có được sau 5 giờ. (kết quả làm tròn đến hàng phần mười).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Lúc đầu có 300 vi khuẩn. Sau 1 giờ số vi khuẩn là 705 con.
Ta có \(\left\{ \begin{array}{l}f\left( 0 \right) = 300 = C.{e^{k.0}} = C\\f\left( 1 \right) = 705 = C.{e^{k.1}} = C.{e^k}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 300\\{e^k} = \frac{{705}}{{300}} = 2,35\end{array} \right.\).
Vậy \(f\left( x \right) = 300.{\left( {2,35} \right)^x}\).
Số lượng vi khuẩn có được sau 5 giờ là \(f\left( 5 \right) = 300.{\left( {2,35} \right)^5} \approx 21501,1\) con.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Trả lời: 0,84
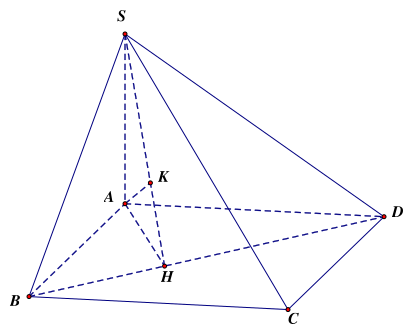
Do \({S_{SAD}} = 3 = \frac{1}{2}SA.AD \Rightarrow SA = \frac{6}{{2\sqrt 3 }} = \sqrt 3 \).
Mặt khác ta có \(d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right)\).
Kẻ \(AH \bot BD,AK \bot SH\) tại \(K\). Suy ra \(d\left( {A,\left( {SBD} \right)} \right) = AK\).
Ta có \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {13} \Rightarrow AH = \frac{{AB.AD}}{{BD}} = \frac{{2\sqrt 3 }}{{\sqrt {13} }} = \frac{{2\sqrt {39} }}{{13}}\).
\( \Rightarrow AK = \frac{{SA.AH}}{{\sqrt {S{A^2} + A{H^2}} }} = \frac{{\sqrt 3 .\frac{{2\sqrt {39} }}{{13}}}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {\frac{{2\sqrt {39} }}{{13}}} \right)}^2}} }} = \frac{{2\sqrt {51} }}{{17}}\).
Vậy \(d\left( {C,\left( {SBD} \right)} \right) = d\left( {A,\left( {SBD} \right)} \right) = \frac{{2\sqrt {51} }}{{17}} \approx 0,84\).
Câu 2
A. \(8,9\).
B. \(7,9\).
C. \(8,6\).
D. \(8,4\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Theo đề ta có \(8 = \log A - \log {A_0}\).
Trận động đất ở Nam Mỹ có cường độ là
\(M = \log 4A - \log {A_0} = \log 4 + \log A - \log {A_0} = \log 4 + 8 \approx 8,6\).
Câu 3
a) \(SA \bot BC\).
b) \(BM \bot \left( {SAC} \right)\).
c) \(BC\) tạo với mặt phẳng \(\left( {SAB} \right)\) một góc có số đo là \(45^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(SA \bot BC\).
B. \(AH \bot BC\).
C. \(AH \bot AC\).
D. \(AH \bot SC\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \({a^{\frac{5}{6}}}\).
B. \({a^{\frac{7}{6}}}\).
C. \({a^{\frac{{11}}{6}}}\).
D. \({a^{\frac{6}{5}}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập