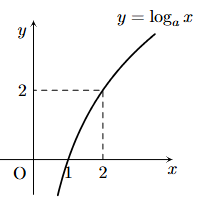B. TRẮC NGHIỆM ĐÚNG - SAI. Thí sinh trả lời từ câu 13 đến câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho phương trình \({9^{2x}}{.27^{{x^2}}} = \frac{1}{3}\).
a) \(x = 0\) là một nghiệm của phương trình.
b) \(x = - 1\)không phải là nghiệm của phương trình.
c) Tổng các nghiệm của phương trình là \(0\).
d) \(x_1^2 + x_2^2 = \frac{{10}}{9}\) với \({x_1},{x_2}\) là hai nghiệm của phương trình trên.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) S, b) S, c) S, d) Đ
a) Thay \(x = 0\) vào phương trình ta được \({9^{2.0}}{.27^{{0^2}}} = \frac{1}{3}\) (sai).
Do đó \(x = 0\)không là nghiệm của phương trình.
b) Thay \(x = - 1\) vào phương trình ta được \({9^{2.\left( { - 1} \right)}}{.27^{{{\left( { - 1} \right)}^2}}} = \frac{1}{3}\) (đúng).
Do đó \(x = - 1\)là nghiệm của phương trình.
c) Ta có \({9^{2x}}{.27^{{x^2}}} = \frac{1}{3}\)\( \Leftrightarrow {3^{4x}}{.3^{3{x^2}}} = {3^{ - 1}}\)\( \Leftrightarrow {3^{4x + 3{x^2}}} = {3^{ - 1}}\)\( \Leftrightarrow 3{x^2} + 4x = - 1\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - \frac{1}{3}\end{array} \right.\).
Do đó tổng các nghiệm là \( - \frac{4}{3}\).
d) \(x_1^2 + x_2^2 = {\left( { - 1} \right)^2} + {\left( {\frac{{ - 1}}{3}} \right)^2} = \frac{{10}}{9}\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đổi 30 cm = 3 dm.
Thể tích của hình lập phương là \({S_1} = {3^3} = 27\) dm3.
Thể tích của khối chóp là \({S_2} = \frac{1}{3}{.3^2}.3 = 9\) dm3.
Thể tích phần không gian bên trong chiếc hộp không bị chiếm bởi mô hình đồ chơi dạng hình chóp là \(S = {S_1} - {S_2} = 27 - 9 = 18\) dm3.
Câu 2
A. \(a = \sqrt 2 \).
B. \(a = \frac{1}{{\sqrt 2 }}\).
C. \(a = \frac{1}{2}\).
D. \(a = 2\).
Lời giải
Đáp án đúng là: A
Vì hàm số \(y = {\log _a}x\) đồng biến nên loại đáp án B, C.
Đồ thị hàm số \(y = {\log _a}x\) đi qua điểm \(\left( {2;2} \right)\) nên \(2 = {\log _a}2 \Rightarrow {a^2} = 2 \Rightarrow a = \sqrt 2 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Tồn tại duy nhất một mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng \(d\) và \(\left( \alpha \right)\) song song với \(\left( P \right)\).
B. Không tồn tại mặt phẳng \(\left( \alpha \right)\)chứa đường thẳng \(d\) và \(\left( \alpha \right)\) song song với \(\left( P \right)\).
C. Tồn tại duy nhất một mặt phẳng \(\left( \alpha \right)\) chứa đường thẳng \(d\) và \(\left( \alpha \right)\) vuông góc với \(\left( P \right)\).
D. Tồn tại duy nhất một đường thẳng \(\Delta \) nằm trên mặt phẳng \(\left( P \right)\) và \(\Delta \) vuông góc với \(d\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập