Cho đườn tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2 cm, IB = 4 cm. Tổng khoảng cách từ tâm O đến dây AB và CD là
A. 4 cm.
B. 1 cm.
C. 3 cm.
D. 2 cm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
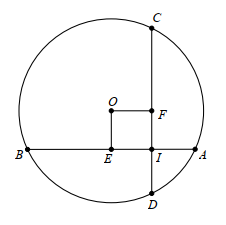
Xét đường tròn (O).
Kẻ OE ⊥ AB tại E suy ra E là trung điểm của AB, kẻ OF ⊥ CD tại F.
Vì dây AB = CD nên OE = OF (hai dây bằng nhau thì cách đều tâm).
Xét tứ giác OEIF có \(\widehat E = \widehat F = \widehat I = 90^\circ \) nên OEIF là hình chữ nhật và OE = OF nên OEIF là hình vuông.
Suy ra OE = OF = EI.
Mà AB = IA + IB = 6 cm nên EB = 3 cm.
Suy ra IE = EB – IB = 1 cm nên OE = OF = 1 cm.
Vậy tổng khoảng cách từ tâm đến hai dây AB, CD là 2 cm.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
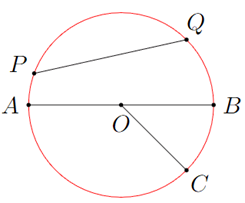
Trong đường tròn (O), AB là đường kính , OC là bán kính và PQ là dây cung không đi qua O.
Do đó AB = 2OC và PQ < AB.
Câu 2
A. MP + NP < MN.
B. MP – NP ≥ MN.
C. MN < MP + NP ≤ 2MN.
D. MN < MP + NP < 2MN.
Lời giải
Đáp án đúng là: D
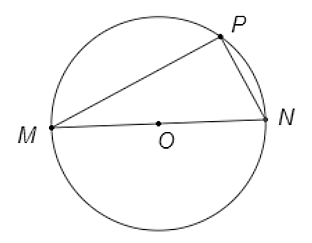
Xét tam giác MNP, có: MN < MP + NP (bất đẳng thức tam giác).
Câu 3
A. AB < R.
B. AB = R.
C. AB ≤ 2R.
D. AB < 2R.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. AB > CD.
B. AB = CD.
C. AB < CD.
D. AB ≤ CD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. AB = 6 cm.
B. AB = 8 cm.
C. AB = 10 cm.
D. AB = 12 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. AB > CD.
B. AB = CD.
C. AB < CD.
D. AB ∕∕ CD.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo