Một hình quạt có chu vi bằng 34 cm và diện tích bằng 66 cm2. Bán kính của hình quạt bằng?
A. R = 5 cm.
B. R = 6 cm hoặc R = 11 cm.
C. R = 7 cm.
D. R = 8 cm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Ta có: \(\left\{ \begin{array}{l}\frac{{lR}}{2} = 66\\l + 2R = 34\end{array} \right.\) khi đó \(\left\{ \begin{array}{l}lR = 132\\l + 2R = 34\end{array} \right.\) hay \(\left\{ \begin{array}{l}2Rl = 264\\l + 2R = 34\end{array} \right.\).
Khi đó l và 2R là nghiệm của phương trình X2 – 34X + 264 = 0 ta được nghiệm kép hay \(\left\{ \begin{array}{l}2R = 22\\l = 12\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}2R = 12\\l = 22\end{array} \right.\) .
Khi đó \(\left\{ \begin{array}{l}R = 11\\l = 12\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}R = 6\\l = 22\end{array} \right.\).
Vậy R = 11 cm hoặc R = 6 cm.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 18π (cm2).
B. 36π (cm2).
C. 18 (cm2).
D. 36 (cm2).
Lời giải
Đáp án đúng là: A
Gọi hình vuông ABCD nội tiếp đường tròn (O) khi đó OA = OB = OC = OD = R.
Do đó, O là giao điểm của AC và BD nên R = \(\frac{{AC}}{2}\).
Xét tam giác vuông ABC ta có:
AB2 + BC2 = AC2
62 + 62 = AC2
Suy ra AC = \(6\sqrt 2 \) suy ra R = \(\frac{{6\sqrt 2 }}{2} = 3\sqrt 2 \).
Diện tích hình tròn (O) là S = πR2 = 18π (cm2).
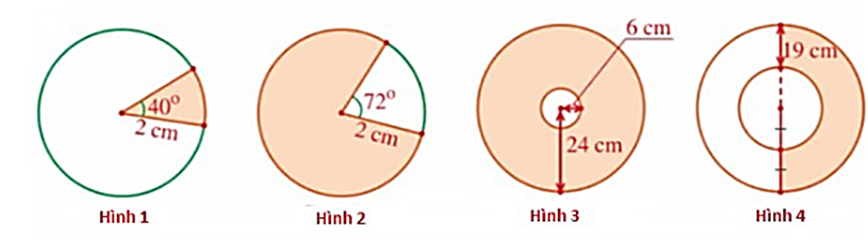
Lời giải
Đáp án đúng là: A
Diện tích S = πR2 = 102π = 100π (cm2).
Câu 3
A. π – \(\sqrt 3 \).
B. 2π – \(2\sqrt 3 \).
C. π – \(3\sqrt 3 \).
D. 2π – \(\sqrt 3 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. R = 5 cm.
B. R = 6 cm.
C. R = 7 cm.
D. R = 8 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 15 cm.
B. 16 cm.
C. 12 cm.
D. 14 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 32π (cm2).
B. 23π (cm2).
C. \(\frac{{32\pi }}{3}\) (cm2).
D. \(\frac{{16\pi }}{3}\) (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập