Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) với \(A\left( {0;3} \right),B\left( {1; - 2} \right),C\left( {5;3} \right)\). Gọi \(H\) là chân đường cao kẻ từ \(A\) xuống \(BC\). Khi đó
a) Một vectơ pháp tuyến của đường cao \(AH\) là \(\overrightarrow {CB} \).
b) Phương trình đường cao \(AH\) là \(4x + 5y - 16 = 0\).
c) Phương trình đường thẳng \(BC\) là \(5x - 4y - 13 = 0\).
d) Độ dài đường cao \(AH\) bằng \(\frac{{10}}{{\sqrt {41} }}\).
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) với \(A\left( {0;3} \right),B\left( {1; - 2} \right),C\left( {5;3} \right)\). Gọi \(H\) là chân đường cao kẻ từ \(A\) xuống \(BC\). Khi đó
a) Một vectơ pháp tuyến của đường cao \(AH\) là \(\overrightarrow {CB} \).
b) Phương trình đường cao \(AH\) là \(4x + 5y - 16 = 0\).
c) Phương trình đường thẳng \(BC\) là \(5x - 4y - 13 = 0\).
d) Độ dài đường cao \(AH\) bằng \(\frac{{10}}{{\sqrt {41} }}\).
Quảng cáo
Trả lời:
a) Đ, b) S, c) Đ, d) S
a) Vì \(AH \bot CB\) nên \(\overrightarrow {CB} \) là một vectơ pháp tuyến của đường cao \(AH\).
b) Đường cao \(AH\) đi qua \(A\left( {0;3} \right)\) và nhận \(\overrightarrow {CB} = \left( { - 4; - 5} \right)\) làm một vectơ pháp tuyến có phương trình là \( - 4x - 5\left( {y - 3} \right) = 0 \Leftrightarrow 4x + 5y - 15 = 0\).
c) Đường thẳng \(BC\) có vectơ chỉ phương \(\overrightarrow {BC} = \left( {4;5} \right)\) nên nhận \(\overrightarrow n = \left( {5; - 4} \right)\) làm vectơ pháp tuyến có phương trình là \(5\left( {x - 1} \right) - 4\left( {y + 2} \right) = 0\) hay \(5x - 4y - 13 = 0\).
d) Ta có \(AH = d\left( {A,BC} \right) = \frac{{\left| {5.0 - 4.3 - 13} \right|}}{{\sqrt {{5^2} + {4^2}} }} = \frac{{25}}{{\sqrt {41} }}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
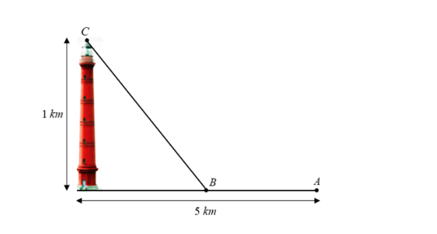
Gọi chều dài đoạn dây điện kéo từ A đến B là \(AB = x\) (km) (\(0 < x < 5\))
Khi đó chiều dài dây điện kéo từ B đến C là \(BC = \sqrt {1 + {{\left( {5 - x} \right)}^2}} = \sqrt {{x^2} - 10x + 26} \) (km)
Tổng số tiền công là \(3\sqrt {{x^2} - 10x + 26} + 2x = 13\) (triệu đồng).
Theo đề ta có: \(3\sqrt {{x^2} - 10x + 26} + 2x = 13\)\( \Leftrightarrow 3\sqrt {{x^2} - 10x + 26} = 13 - 2x\).
Bình phương hai về của phương trình ta được:
\(9\left( {{x^2} - 10x + 26} \right) = 169 - 52x + 4{x^2}\)\( \Leftrightarrow 5{x^2} - 38x + 65 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = \frac{{13}}{5}\end{array} \right.\).
Thay các giá trị của \(x\) vào phương trình ban đầu và kết hợp với điều kiện ta thấy \(x = \frac{{13}}{5}\) là nghiệm.
Khi đó \(AB = x = \frac{{13}}{5} \Rightarrow BC = \frac{{13}}{5}\).
Vậy tổng chiều dài dây điện đã kéo từ A đến C là \(AB + BC = \frac{{26}}{5} = 5,2\) (km).
Câu 2
Lời giải
Đáp án đúng là: B
Thay lần lượt các giá trị của \(x\) vào phương trình ta thấy \(x = 1\) là nghiệm của phương trình.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 1\).
B. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.