Câu hỏi:
14/02/2025 1,625
Gia đình ông Ba đi du lịch bằng xe hơi 7 chỗ. Họ phải lái xe \[100{\rm{ km}}\] trên đường thường và 240 km trên đường cao tốc. Tốc độ trên đường cao tốc hơn tốc độ trên đường thường là \[50\% .\] Gọi \(r\) (km/giờ) là tốc độ trên đường thường.
a) Hãy viết biểu thức tính thời gian mà gia đình ông Ba phải đi.
b) Hãy tính thời gian gia đình ông Ba phải đi nếu họ lái xe đúng theo giới hạn quy định tốc độ cho phép xe ô tô dưới 30 chỗ là 40 km/giờ khi lưu thông trên đường trong khu vực đông dân cư.
Gia đình ông Ba đi du lịch bằng xe hơi 7 chỗ. Họ phải lái xe \[100{\rm{ km}}\] trên đường thường và 240 km trên đường cao tốc. Tốc độ trên đường cao tốc hơn tốc độ trên đường thường là \[50\% .\] Gọi \(r\) (km/giờ) là tốc độ trên đường thường.
a) Hãy viết biểu thức tính thời gian mà gia đình ông Ba phải đi.
b) Hãy tính thời gian gia đình ông Ba phải đi nếu họ lái xe đúng theo giới hạn quy định tốc độ cho phép xe ô tô dưới 30 chỗ là 40 km/giờ khi lưu thông trên đường trong khu vực đông dân cư.
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tốc độ trên đường cao tốc là: \[r + 50\% \cdot r = 1,5r\] (giờ)
Thời gian gia đình ông Ba đi trên đoạn đường bình thường là: \(\frac{{100}}{r}\) (giờ).
Thời gian gia đình ông Ba đi trên đoạn đường cao tốc là: \(\frac{{240}}{{1,5r}} = \frac{{160}}{r}\) (giờ).
Thời gian gia đình ông Ba phải đi là: \(\frac{{100}}{r} + \frac{{160}}{r} = \frac{{260}}{r}\) (giờ).
b) Nếu họ lái xa đúng giới hạn ghi trên biển chỉ đường thì \(r = 40\) (km/giờ) và khi đó thời gian gia đình ông Ba phải đi là: \(\frac{{260}}{{40}} = 6,5\) (giờ) = 6 giờ 30 phút.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \(1 - {x^2} = - \left( {{x^2} - 1} \right) = - \left( {x - 1} \right)\left( {x + 1} \right).\)
Khi đó, điều kiện xác định của biểu thức \(B\) là \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\\1 - {x^2} \ne 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\\ - \left( {x - 1} \right)\left( {x + 1} \right) \ne 0\end{array} \right.,\) tức là \(\left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right..\)
Vậy để \(B\) xác định thì \(x \ne 1\) và \(x \ne - 1.\)
b) Với \(x \ne 1\) và \(x \ne - 1\) ta có:
\(B = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{4}{{1 - {x^2}}}\)\( = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} - \frac{4}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\( = \frac{{{{\left( {x + 1} \right)}^2} - {{\left( {x - 1} \right)}^2} - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{{\left( {{x^2} + 2x + 1} \right) - \left( {{x^2} - 2x + 1} \right) - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\( = \frac{{4x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{{4\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{4}{{x + 1}}\).
Vì vậy với \(x \ne 1\) và \(x \ne - 1\) thì \(B = \frac{4}{{x + 1}}.\)
Với \(x = - \frac{1}{2}\) thoả mãn điều kiện xác định, thay vào biểu thức \(B = \frac{4}{{x + 1}},\) ta được:
\(B = \frac{4}{{ - \frac{1}{2} + 1}} = \frac{4}{{\frac{1}{2}}} = 8.\)
Vậy với \(x = - \frac{1}{2}\) thì \(B = 8.\)
c) Với \(x \ne 1\) và \(x \ne - 1\) thì \(B = \frac{4}{{x + 1}}.\)
Với \(x\) là số nguyên, để \(B\) nhận giá trị nguyên thì \(x + 1\) là ước của \(4.\)
Mà Ư\(\left( 4 \right) = \left\{ {1;\,\, - 1;\,\,2;\,\, - 2;\,\,4;\,\, - 4} \right\}.\)
Ta có bảng sau:
|
\(x + 1\) |
\(1\) |
\( - 1\) |
\(2\) |
\( - 2\) |
\(4\) |
\( - 4\) |
|
\(x\) |
\(0\) |
\( - 2\) |
\(1\) |
\( - 3\) |
\(3\) |
\( - 5\) |
Do đó: \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,1;\,\,3} \right\}.\)
Mà \(x \ne 1\) và \(x \ne - 1\) nên \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,3} \right\}.\)
Vậy để \(B\) nhận giá trị nguyên thì \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,3} \right\}.\)
Lời giải
|
Từ \(D\) vẽ \(Dx \bot CD\) cắt tia \(AB\) tại \(E.\) Xét tứ giác \(BCDE\) có \(\widehat {BCD} = \widehat {CDE} = \widehat {CBE} = 90^\circ \) nên \(BCDE\) là hình chữ nhật. Do đó \(DE = BC = 12{\rm{\;cm}},\,\,BE = CD = 6{\rm{\;cm}}.\) Có \(AE = AB + BE = 10 + 6 = 16{\rm{\;cm}}.\) Áp dụng định lí Pythagore cho \(\Delta ADE\) vuông tại \(E,\) ta được: \(A{D^2} = A{E^2} + D{E^2} = {16^2} + {12^2} = 400.\) Suy ra \(AD = \sqrt {400} = 20{\rm{\;cm}}.\) |
 |
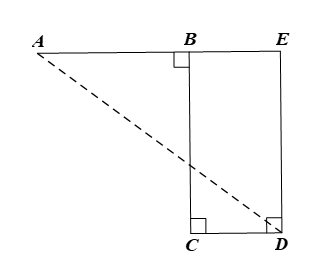Thời gian viên bi lăn theo đoạn thẳng \(AD\) là \(\frac{{20 \cdot 21}}{{28}} = 15\) (giây).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận