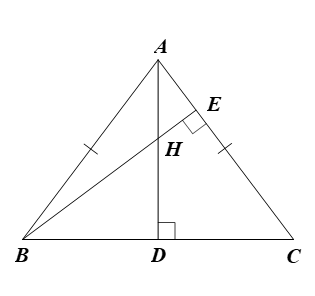
Tam giác \(ABC\) cân tại \(A,\) \(AB = AC = 100{\rm{\;cm}},\) \(BC = 120{\rm{\;cm}},\) các đường cao \(AD\) và \(BE\) cắt nhau tại \(H.\)
a) Tính độ dài đoạn thẳng \(AD.\) b) Chứng minh
c) Tính độ dài đoạn thẳng \(HD,\,\,HB.\) d) Tính độ dài đoạn thẳng \(HE.\)
Tam giác \(ABC\) cân tại \(A,\) \(AB = AC = 100{\rm{\;cm}},\) \(BC = 120{\rm{\;cm}},\) các đường cao \(AD\) và \(BE\) cắt nhau tại \(H.\)
a) Tính độ dài đoạn thẳng \(AD.\) b) Chứng minh
c) Tính độ dài đoạn thẳng \(HD,\,\,HB.\) d) Tính độ dài đoạn thẳng \(HE.\)
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
|
a) Xét \(\Delta ABC\) cân tại \(A\) có đường cao \(AD\) nên đồng thời là đường trung tuyến, đo dó \(BD = CD = \frac{1}{2}BC = \frac{1}{2} \cdot 120 = 60{\rm{\;cm}}.\) Áp dụng định lí Pythagore cho \(\Delta ABD\) vuông tại \(D,\) ta có: |
 |
\(A{B^2} = A{D^2} + B{D^2},\) suy ra \(A{D^2} = A{B^2} - B{D^2} = {100^2} - {60^2} = 6\,\,400.\)
Do đó \(AD = \sqrt {6\,\,400} = 80{\rm{\;cm}}.\)
b) Xét \(\Delta BDH\) và \(\Delta ADC\) có:
\(\widehat {BDH} = \widehat {ADC} = 90^\circ \) và \(\widehat {HBD} = \widehat {DAC}\) (cùng phụ với \(\widehat {ECB}).\)
Do đó (g.g).
c) Theo câu b, suy ra \(\widehat {BHD} = \widehat {ACD}\) (hai góc tương ứng).
Mà \(\widehat {ABD} = \widehat {ACD}\) (do \(\Delta ABC\) cân tại \(A),\) nên \(\widehat {BHD} = \widehat {ABD}.\)
Xét \(\Delta BDH\) và \(\Delta ADB\) có:
\(\widehat {BDH} = \widehat {ADB} = 90^\circ \) và \(\widehat {BHD} = \widehat {ABD}\)
Do đó (g.g).
Suy ra \(\frac{{BD}}{{AD}} = \frac{{BH}}{{AB}} = \frac{{DH}}{{DB}}\) (tỉ số cạnh tương ứng).
Hay \(\frac{{60}}{{80}} = \frac{{BH}}{{100}} = \frac{{DH}}{{60}},\) suy ra \(BH = \frac{{60 \cdot 100}}{{80}} = 75{\rm{\;cm}}\) và \(DH = \frac{{60 \cdot 60}}{{80}} = 45{\rm{\;cm}}.\)
d) Ta có \(AH = AD - DH = 80 - 45 = 35{\rm{\;cm}}.\)
Xét \(\Delta BDH\) và \(\Delta BEC\) có:
\(\widehat {BDH} = \widehat {BEC} = 90^\circ \) và \(\widehat {EBC}\) là góc chung.
Do đó (g.g).
Xét \(\Delta BDH\) và \(\Delta AEH\) có:
\(\widehat {BDH} = \widehat {AHE} = 90^\circ \) và \(\widehat {BHD} = \widehat {AHE}\) (đối đỉnh).
Do đó (g.g).
Mà nên
Do đó \(\frac{{HE}}{{BD}} = \frac{{AH}}{{AB}}\) (tỉ số cạnh tương ứng), hay \(\frac{{HE}}{{60}} = \frac{{35}}{{100}},\) suy ra \(HE = \frac{{60 \cdot 35}}{{100}} = 21{\rm{\;}}\left( {{\rm{cm}}} \right).\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \(1 - {x^2} = - \left( {{x^2} - 1} \right) = - \left( {x - 1} \right)\left( {x + 1} \right).\)
Khi đó, điều kiện xác định của biểu thức \(B\) là \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\\1 - {x^2} \ne 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\\ - \left( {x - 1} \right)\left( {x + 1} \right) \ne 0\end{array} \right.,\) tức là \(\left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right..\)
Vậy để \(B\) xác định thì \(x \ne 1\) và \(x \ne - 1.\)
b) Với \(x \ne 1\) và \(x \ne - 1\) ta có:
\(B = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{4}{{1 - {x^2}}}\)\( = \frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} - \frac{4}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\( = \frac{{{{\left( {x + 1} \right)}^2} - {{\left( {x - 1} \right)}^2} - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{{\left( {{x^2} + 2x + 1} \right) - \left( {{x^2} - 2x + 1} \right) - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)
\( = \frac{{4x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{{4\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\)\( = \frac{4}{{x + 1}}\).
Vì vậy với \(x \ne 1\) và \(x \ne - 1\) thì \(B = \frac{4}{{x + 1}}.\)
Với \(x = - \frac{1}{2}\) thoả mãn điều kiện xác định, thay vào biểu thức \(B = \frac{4}{{x + 1}},\) ta được:
\(B = \frac{4}{{ - \frac{1}{2} + 1}} = \frac{4}{{\frac{1}{2}}} = 8.\)
Vậy với \(x = - \frac{1}{2}\) thì \(B = 8.\)
c) Với \(x \ne 1\) và \(x \ne - 1\) thì \(B = \frac{4}{{x + 1}}.\)
Với \(x\) là số nguyên, để \(B\) nhận giá trị nguyên thì \(x + 1\) là ước của \(4.\)
Mà Ư\(\left( 4 \right) = \left\{ {1;\,\, - 1;\,\,2;\,\, - 2;\,\,4;\,\, - 4} \right\}.\)
Ta có bảng sau:
|
\(x + 1\) |
\(1\) |
\( - 1\) |
\(2\) |
\( - 2\) |
\(4\) |
\( - 4\) |
|
\(x\) |
\(0\) |
\( - 2\) |
\(1\) |
\( - 3\) |
\(3\) |
\( - 5\) |
Do đó: \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,1;\,\,3} \right\}.\)
Mà \(x \ne 1\) và \(x \ne - 1\) nên \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,3} \right\}.\)
Vậy để \(B\) nhận giá trị nguyên thì \(x \in \left\{ { - 5;\,\, - 3;\,\, - 2;\,\,0;\,\,3} \right\}.\)
Lời giải
a) Tốc độ trên đường cao tốc là: \[r + 50\% \cdot r = 1,5r\] (giờ)
Thời gian gia đình ông Ba đi trên đoạn đường bình thường là: \(\frac{{100}}{r}\) (giờ).
Thời gian gia đình ông Ba đi trên đoạn đường cao tốc là: \(\frac{{240}}{{1,5r}} = \frac{{160}}{r}\) (giờ).
Thời gian gia đình ông Ba phải đi là: \(\frac{{100}}{r} + \frac{{160}}{r} = \frac{{260}}{r}\) (giờ).
b) Nếu họ lái xa đúng giới hạn ghi trên biển chỉ đường thì \(r = 40\) (km/giờ) và khi đó thời gian gia đình ông Ba phải đi là: \(\frac{{260}}{{40}} = 6,5\) (giờ) = 6 giờ 30 phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo