Cho hàm số \[y = \left( {3--m} \right)x + 3m + 2.\] Tìm các giá trị của \[m\] để
a) hàm số đã cho là hàm số bậc nhất.
b) đồ thị hàm số đã cho là đường thẳng đi qua điểm \[\left( {1;{\rm{ }}3} \right).\]
c) đồ thị hàm số đã cho là đường thẳng cắt đường thẳng \[y = x--1\] tại một điểm nằm trên trục tung.
Cho hàm số \[y = \left( {3--m} \right)x + 3m + 2.\] Tìm các giá trị của \[m\] để
a) hàm số đã cho là hàm số bậc nhất.
b) đồ thị hàm số đã cho là đường thẳng đi qua điểm \[\left( {1;{\rm{ }}3} \right).\]
c) đồ thị hàm số đã cho là đường thẳng cắt đường thẳng \[y = x--1\] tại một điểm nằm trên trục tung.
Quảng cáo
Trả lời:
a) Để hàm số đã cho là hàm số bậc nhất thì \(3 - m \ne 0,\) hay \(m \ne 3.\)
b) Để đường thẳng \[y = \left( {3--m} \right)x + 3m + 2\] đi qua điểm \[\left( {1;3} \right)\] thì \(x = 1\) và \(y = 3\) thỏa mãn hàm số trên.
Do đó ta có: \[3 = \left( {3--m} \right) \cdot 1 + 3m + 2\]
\[3 = 3--m + 3m + 2\]
\[2m = - 2\]
\(m = - 1.\)
Vậy \(m = - 1\) thỏa mãn yêu cầu đề bài.
c) Để đường thẳng \[y = \left( {3--m} \right)x + 3m + 2\] cắt đường thẳng \[y = x--1\] thì \(3 - m \ne 1,\) do đó \(m \ne 2.\)
Gọi \(A\left( {{x_A};{y_A}} \right)\) là giao điểm của hai đường thẳng.
Để hai đường thẳng trên cắt nhau tại điểm \(A\left( {{x_A};{y_A}} \right)\) nằm trên trục tung thì \({x_A} = 0.\)
Thay \({x_A} = 0\) vào hàm số \[y = x--1\] ta được \({y_A} = 0 - 1 = - 1.\)
Thay \({x_A} = 0\) và \({y_A} = - 1\) vào hàm số \[y = \left( {3--m} \right)x + 3m + 2\] ta được:
\[ - 1 = \left( {3--m} \right) \cdot 0 + 3m + 2\]
\[ - 1 = 3m + 2\]
\[m = - 1\] (thỏa mãn \(m \ne 2).\)
Vậy \(m = - 1\) thỏa mãn yêu cầu đề bài.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Công thức biểu thị số tiền \[y\] (đồng) thu được khi bán \[x\,\,\left( {{\rm{kg}}} \right)\] thanh long ruột đỏ loại I là:
\[y = 32\,\,000x.\]
Khi đó \[y\] là hàm số của \[x\], vì với mỗi giá trị của \[x\] chỉ xác định đúng một giá trị của \[y\].
b) Số tiền thu được khi bán 8 kg thanh long ruột đỏ loại I là:
32000 . 8 = 256 000 (đồng).
Vậy số tiền thu được khi bán 8 kg thanh long ruột đỏ loại I là 256 000 đồng.
Lời giải
|
a) Trong \(\Delta ABC\) có các đường trung tuyến \[BD,{\rm{ }}CE\] nên \[D\] là trung điểm của \[AC,\] \[E\] là trung điểm của \[AB\] nên \[ED\] là đường trung bình của \(\Delta ABC.\) Suy ra \(ED = \frac{1}{2}BC\) và \[ED\,{\rm{//}}\,BC\] (tính chất đường trung bình của tam giác). |
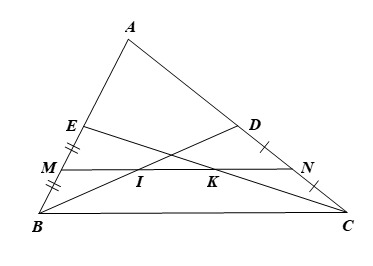 |
b) Ta có: \[E\] là trung điểm của \[AB\] nên \(AE = EB = \frac{1}{2}AB.\)
Mà \[M\] là trung điểm của \[EB\] nên \(EM = MB = \frac{1}{2}EB = \frac{1}{4}AB\) hay \(\frac{{MB}}{{AB}} = \frac{1}{4}.\)
Tương tự, ta cũng có \(NC = \frac{1}{4}AC\) hay \(\frac{{NC}}{{AC}} = \frac{1}{4}.\)
Suy ra \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\,\,\left( { = \frac{1}{4}} \right).\)
Xét \(\Delta ABC\) có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) nên \[MN\,{\rm{//}}\,BC\] (định lí Thalès đảo).
c) Ta có \[MN\,{\rm{//}}\,BC\] (câu b) và \[ED\,{\rm{//}}\,BC\] (câu a) nên \[ED\,{\rm{//}}\,MN\,{\rm{//}}\,BC.\]
Xét \(\Delta BDE\) có \[M\] là trung điểm của \[EB\] và \[MI\,{\rm{//}}\,ED\] (do \[ED\,{\rm{//}}\,MN)\]
Suy ra \[I\] là trung điểm của \[BD\] hay \[IB = ID.\]
Khi đó \[MI\] là đường trung bình của \(\Delta BDE\) nên \(MI = \frac{1}{2}ED.\)
Tương tự, trong DCDE ta cũng có \(KN = \frac{1}{2}ED,\) trong DBCE có \(MK = \frac{1}{2}BC.\)
Ta có \(IK = MK - MI = \frac{1}{2}BC - \frac{1}{2}ED = ED - \frac{1}{2}ED = \frac{1}{2}ED\).
Do đó \(MI = IK = KN = \frac{1}{2}ED\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Với số liệu được ghi trên hình vẽ bên dưới. Tính khoảng cách \[CD\] từ con tàu đến trạm quan trắc đặt tại điểm \[C.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid31-1739678853.png)