Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án ( Đề 6)
21 người thi tuần này 4.6 2.5 K lượt thi 5 câu hỏi 50 phút
🔥 Đề thi HOT:
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
20 câu trắc nghiệm Toán 8 Kết nối tri thức Ôn tập chương I (Đúng sai - trả lời ngắn) có đáp án
Bộ 5 đề thi cuối kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
Bộ 10 đề thi Cuối kì 1 Toán 8 Kết nối tri thức có đáp án - Đề 1
Đề thi Toán lớp 8 Giữa học kì 2 năm 2020 - 2021 có đáp án (Đề 1)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) Công thức biểu thị số tiền \[y\] (đồng) thu được khi bán \[x\,\,\left( {{\rm{kg}}} \right)\] thanh long ruột đỏ loại I là:
\[y = 32\,\,000x.\]
Khi đó \[y\] là hàm số của \[x\], vì với mỗi giá trị của \[x\] chỉ xác định đúng một giá trị của \[y\].
b) Số tiền thu được khi bán 8 kg thanh long ruột đỏ loại I là:
32000 . 8 = 256 000 (đồng).
Vậy số tiền thu được khi bán 8 kg thanh long ruột đỏ loại I là 256 000 đồng.
Lời giải
a) Để hàm số đã cho là hàm số bậc nhất thì \(3 - m \ne 0,\) hay \(m \ne 3.\)
b) Để đường thẳng \[y = \left( {3--m} \right)x + 3m + 2\] đi qua điểm \[\left( {1;3} \right)\] thì \(x = 1\) và \(y = 3\) thỏa mãn hàm số trên.
Do đó ta có: \[3 = \left( {3--m} \right) \cdot 1 + 3m + 2\]
\[3 = 3--m + 3m + 2\]
\[2m = - 2\]
\(m = - 1.\)
Vậy \(m = - 1\) thỏa mãn yêu cầu đề bài.
c) Để đường thẳng \[y = \left( {3--m} \right)x + 3m + 2\] cắt đường thẳng \[y = x--1\] thì \(3 - m \ne 1,\) do đó \(m \ne 2.\)
Gọi \(A\left( {{x_A};{y_A}} \right)\) là giao điểm của hai đường thẳng.
Để hai đường thẳng trên cắt nhau tại điểm \(A\left( {{x_A};{y_A}} \right)\) nằm trên trục tung thì \({x_A} = 0.\)
Thay \({x_A} = 0\) vào hàm số \[y = x--1\] ta được \({y_A} = 0 - 1 = - 1.\)
Thay \({x_A} = 0\) và \({y_A} = - 1\) vào hàm số \[y = \left( {3--m} \right)x + 3m + 2\] ta được:
\[ - 1 = \left( {3--m} \right) \cdot 0 + 3m + 2\]
\[ - 1 = 3m + 2\]
\[m = - 1\] (thỏa mãn \(m \ne 2).\)
Vậy \(m = - 1\) thỏa mãn yêu cầu đề bài.
Lời giải
a) Mức giá khi lượng cung bằng lượng cầu là giá trị \[{x_0}\] thỏa mãn:
\[--600 + 10{x_0} = 1{\rm{ }}200--20{x_0}\]
\[30{x_0} = 1{\rm{ }}800\]
\[{x_0} = 60\]
Vậy mức giá cân bằng là 60 nghìn đồng.
b) Đồ thị hàm số \[S\left( p \right)\] đi qua hai điểm \[\left( {0;--600} \right)\] và \[\left( {60;{\rm{ }}0} \right).\]
Đồ thị hàm số \[D\left( p \right)\] đi qua hai điểm \[\left( {0;{\rm{ }}1{\rm{ }}200} \right)\] và \[\left( {60;{\rm{ }}0} \right).\]
Đồ thị của hai hàm số được vẽ trong hình dưới:
![Giả sử rằng lượng cung \[S\] và lượng cầu \[D\] về áo phông tại một buổi biểu diễn được cho bởi các hàm số sau: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid28-1739678734.png)
c) Từ đồ thị trên, ta thấy khi giá của mỗi chiếc áo lớn hơn 60 nghìn đồng thì lượng cung lớn hơn lượng cầu. Khi đó sẽ có một lượng áo phông bị tồn kho (do không bán được).
Lời giải
|
a) Trong \(\Delta ABC\) có các đường trung tuyến \[BD,{\rm{ }}CE\] nên \[D\] là trung điểm của \[AC,\] \[E\] là trung điểm của \[AB\] nên \[ED\] là đường trung bình của \(\Delta ABC.\) Suy ra \(ED = \frac{1}{2}BC\) và \[ED\,{\rm{//}}\,BC\] (tính chất đường trung bình của tam giác). |
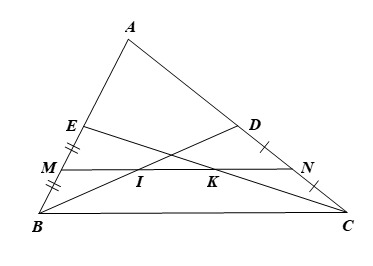 |
b) Ta có: \[E\] là trung điểm của \[AB\] nên \(AE = EB = \frac{1}{2}AB.\)
Mà \[M\] là trung điểm của \[EB\] nên \(EM = MB = \frac{1}{2}EB = \frac{1}{4}AB\) hay \(\frac{{MB}}{{AB}} = \frac{1}{4}.\)
Tương tự, ta cũng có \(NC = \frac{1}{4}AC\) hay \(\frac{{NC}}{{AC}} = \frac{1}{4}.\)
Suy ra \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\,\,\left( { = \frac{1}{4}} \right).\)
Xét \(\Delta ABC\) có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) nên \[MN\,{\rm{//}}\,BC\] (định lí Thalès đảo).
c) Ta có \[MN\,{\rm{//}}\,BC\] (câu b) và \[ED\,{\rm{//}}\,BC\] (câu a) nên \[ED\,{\rm{//}}\,MN\,{\rm{//}}\,BC.\]
Xét \(\Delta BDE\) có \[M\] là trung điểm của \[EB\] và \[MI\,{\rm{//}}\,ED\] (do \[ED\,{\rm{//}}\,MN)\]
Suy ra \[I\] là trung điểm của \[BD\] hay \[IB = ID.\]
Khi đó \[MI\] là đường trung bình của \(\Delta BDE\) nên \(MI = \frac{1}{2}ED.\)
Tương tự, trong DCDE ta cũng có \(KN = \frac{1}{2}ED,\) trong DBCE có \(MK = \frac{1}{2}BC.\)
Ta có \(IK = MK - MI = \frac{1}{2}BC - \frac{1}{2}ED = ED - \frac{1}{2}ED = \frac{1}{2}ED\).
Do đó \(MI = IK = KN = \frac{1}{2}ED\).
Lời giải
Hướng dẫn giải
Ta có: \[\widehat {ACD} = \widehat {ABE}\] mà hai góc ở vị trí đồng vị nên \[CD{\rm{ // }}BE.\]
Ta có \(AC = AB + BC = 200 + 400 = 600\,\,{\rm{(m)}}\).
Theo hệ quả định lí Thalès, ta có: \[\frac{{CD}}{{BE}} = \frac{{AC}}{{AB}}\].
Hay \[\frac{{CD}}{{120}} = \frac{{600}}{{200}}\] suy ra \[CD = \frac{{600 \cdot 120}}{{200}} = 360\,\,({\rm{m)}}\].
Vậy khoảng cách từ con tàu đến trạm quan trắc là 360 m.

![Với số liệu được ghi trên hình vẽ bên dưới. Tính khoảng cách \[CD\] từ con tàu đến trạm quan trắc đặt tại điểm \[C.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/02/blobid31-1739678853.png)