Cho đường tròn \[\left( O \right)\] đường kính \[AB.\] Gọi \[H\] là điểm nằm giữa \[O\] và \[B.\] Kẻ dây \[CD\] vuông góc với \[AB\] tại \[H.\] Trên cung nhỏ \[AC\] lấy điểm \[E\] bất kỳ \[\left( E \right.\] khác \[A\] và \[\left. C \right).\] Kẻ \[CK\] vuông góc với \[AE\] tại \[K.\] Đường thẳng \[DE\] cắt \[CK\] tại \[F.\]
a) Chứng minh tứ giác \[AHCK\] là tứ giác nội tiếp.
b) Chứng minh \[KH\] song song với \[ED\] và tam giác \[ACF\] là tam giác cân.
c) Tìm vị trí của điểm \[E\] để diện tích tam giác \[ADF\] lớn nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
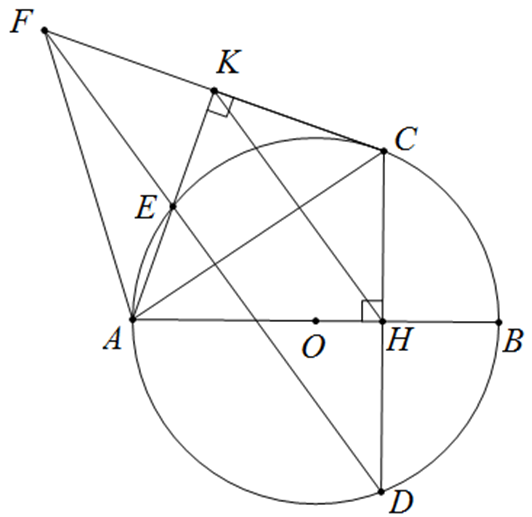
a) Vì \(CK \bot AK\) nên \(\widehat {AKC} = 90^\circ .\) Vì \(CH \bot AB\) tại \[H\] nên \(\widehat {AHC} = 90^\circ .\)
Gọi \(I\)là trung điểm \(AC\).
\(\Delta AKC\)có \(KI\) là trung tuyến ứng với cạnh huyền \(AC\) nên \(KI = OA = OC = \frac{1}{2}AC.\)
\(\Delta AHC\) có \(HI\) là trung tuyến ứng với cạnh huyền\(AC\) nên \(HI = IA = IC = \frac{1}{2}AC.\)
Do đó \(IA = IK = IC = IH.\)
Vậy bốn điểm
\(A,\,\,H,\,\,C,\,\,K\) cùng nằm trên cùng một đường tròn tâm \(I\) hay tứ giác \[AHCK\] nội tiếp.
b) Vì \[AHCK\] là tứ giác nội tiếp nên \(\widehat {CHK} = \widehat {CAK} = \widehat {CAE}\) (góc nội tiếp cùng chắn cung \[KC).\]
Lại có \[ADCE\]nội tiếp nên \(\widehat {CAE} = \widehat {CDE}\) (góc nội tiếp cùng chắn cung \[EC).\]
Từ đó suy ra \(\widehat {CHK} = \widehat {CDE}\) nên \(HK\,{\rm{//}}\,DE\) (đpcm).
Do \(HK\,{\rm{//}}\,DE\), mà \[H\] là trung điểm \[CD\] (quan hệ vuông góc của đường kính \[AB\] với dây \[CD\] tại \[H).\]
Suy ra \[HK\] là đường trung bình của tam giác \[CDF\] nên \[K\] là trung điểm \[FC\].
Tam giác \[AFC\] có \[AK\] là đường cao đồng thời cũng là trung tuyến.
Do đó tam giác \[CAF\]là tam giác cân tại \[K\] (đpcm).
c) Tam giác \[FAC\] cân tại \[A\] nên \[AF = AC.\]
Dễ thấy tam giác \[ACD\] cân tại \[A\] nên \[AC = AD\].
Từ đó suy ra \[AF = AD\] hay tam giác \[AFD\] cân tại \[A\], hạ \[DI \bot AF\] .
Ta có \({S_{AFD}} = \frac{1}{2}DI \cdot AF = \frac{1}{2}DI \cdot AC\).
Do \[AC\] không đổi nên \({S_{AFD}}\) lớn nhất khi và chỉ khi \[DI\] lớn nhất.
Trong tam giác vuông \[AID\] ta có:
\(ID \le AD = AC\) hay \({S_{AFD}} = \frac{1}{2}DI \cdot AF = \frac{1}{2}DI \cdot AC \le \frac{{A{C^2}}}{2}\).
Dấu xảy ra khi và chỉ khi \(I \equiv A\), khi đó \[\widehat {DAF} = 90^\circ \] nên tam giác \[ADF\] vuông cân tại \[A\], suy ra \(\widehat {EBA} = \widehat {EDA} = 45^\circ \) hay \[E\] là điểm chính giữa cung \[AB.\]
Vậy để diện tích tam giác \[ADF\] lớn nhất thì \[E\] là điểm chính giữa cung \[AB.\]
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Nón Huế là một hình nón có đường kính đáy bằng \[40\,\,{\rm{cm,}}\] độ dài đường sinh là \[30\,\,{\mathop{\rm cm}\nolimits} \]. Người ta lát mặt xung quanh hình nón bằng ba lớp lá khô. Tính d (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/03/blobid0-1741012868.png)
Lời giải
Hướng dẫn giải
Đáp số: 5656.
Chiếc nón Huế là một hình nón có đường kính đáy
\(d = 40\,\,{\rm{cm}}\) nên độ dài bán kính đáy là:
\(R = \frac{d}{2} = \frac{{40}}{2} = 20\,\,\left( {{\rm{cm}}} \right)\).
Độ dài đường sinh \(l = 30\,\,cm\).
Diện tích xung quanh của hình nón này là: \[S = \pi Rl = \pi \cdot 20 \cdot 30 = 600\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Vì người ta lợp nón bằng 3 lớp lá, nên diện tích lá cần dùng để tạo nên một chiếc nón Huế sẽ là:
\(600\pi \cdot 3 = 1800\pi \approx 5655\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy diện tích lá cần dùng để tạo nên một chiếc nón Huế khoảng \(5655\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
Câu 2
B. Tự luận
1. Sau khi điều tra về số học sinh trong \[100\] lớp học (đơn vị: học sinh), người ta có bảng tần số ghép nhóm như ở bảng sau:
|
Nhóm |
\[\left[ {36\,\,;\,\,38} \right)\] |
\[\left[ {38\,\,;\,\,40} \right)\] |
\[\left[ {40\,\,;\,\,42} \right)\] |
\[\left[ {42\,\,;\,\,44} \right)\] |
\[\left[ {44\,\,;\,\,46} \right)\] |
|
Tần số \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
a) Tìm tần số tương đối của mỗi nhóm đó.
b) Lập bảng tần số tương đối ghép nhóm và vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột của mẫu số liệu ghép nhóm đó.
2. Viết một số tự nhiên có chẵn có ba chữ số. Xét biến cố \(A:\) “Số tự nhiên là bội của 11”. Tính xác suất của biến cố \(A.\)
Lời giải
Hướng dẫn giải
1. a) Tần số tương đối của các nhóm lần lượt là: \[{f_1} = \frac{{20}}{{100}} \cdot 100\% = 20\% \]; \[{f_2} = \frac{{15}}{{100}} \cdot 100\% = 15\% \];
\[{f_3} = \frac{{25}}{{100}} \cdot 100\% = 25\% \];\[{f_4} = \frac{{30}}{{100}} \cdot 100\% = 30\% \]; \[{f_5} = \frac{{10}}{{100}} \cdot 100\% = 10\% \]
b) Bảng tần số tương đối của mỗi nhóm
|
Nhóm |
\[\left[ {36\,;\,38} \right)\] |
\[\left[ {38\,;40} \right)\] |
\[\left[ {40\,;42} \right)\] |
\[\left[ {42\,;\,44} \right)\] |
\[\left[ {44\,;46} \right)\] |
|
Tần số tương đối \[\left( n \right)\] |
\[20\] |
\[15\] |
\[25\] |
\[30\] |
\[10\] |
Biểu đồ cột của mẫu số liệu ghép nhóm:
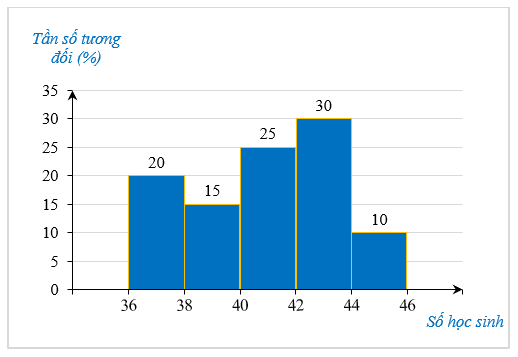
2. a) Số cách viết chữ số hàng trăm là 9 cách (các số từ 1 đến 9).
Số cách viết chữ số hàng chục là 10 cách (các số từ 0 đến 0).
Số cách viết các chữ hàng đơn vị để là số chẵn 5 cách (các số 0; 2; 4; 6; 8).
Vậy số phần tử của tập hợp \(\Omega \) là: \(9.10.5 = 450\) (phần tử)
b) Các số là bội của 11 là \(\left\{ {110\,;\,\,132\,;\,\,154\,;\,\, \ldots ;\,\,990} \right\}\).
Số phần tử tập hợp các số chia hết cho 11 gồm 3 chữ số chẵn là \(\left( {990 - 110} \right):22 + 1 = 41\).
Xác suất để số viết ra là số chia hết cho 11 là \(\frac{{41}}{{450}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
100dayyu Dao
tại sao ac lại cố định vậy ạ