Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại.
Sau đây là kết quả của mỗi ván chơi:
Lần thứ
1
2
3
4
5
6
7
8
9
10
Dũng
L
B
B
K
L
B
K
B
K
K
Nam
B
K
L
L
K
B
L
K
L
B
Tính xác suất thực nghiệm của các sự kiện sau:
a) “Dũng ra búa”. b) “Dũng thắng”. c) “Nam không thua Dũng”.
Hai bạn Dũng và Nam chơi 1 ván oẳn tù tì gồm 10 lần theo luật chơi: Búa (B) thắng Kéo (K); Kéo (K) thắng Lá (L), Lá (L) thắng Búa (B) và hòa nhau nếu cùng loại.
Sau đây là kết quả của mỗi ván chơi:
|
Lần thứ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Dũng |
L |
B |
B |
K |
L |
B |
K |
B |
K |
K |
|
Nam |
B |
K |
L |
L |
K |
B |
L |
K |
L |
B |
Tính xác suất thực nghiệm của các sự kiện sau:
a) “Dũng ra búa”. b) “Dũng thắng”. c) “Nam không thua Dũng”.
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
b) Ta có bảng thống kê sau:
|
Lần thứ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Dũng |
L |
B |
B |
K |
L |
B |
K |
B |
K |
K |
|
Nam |
B |
K |
L |
L |
K |
B |
L |
K |
L |
B |
|
Kết quả ván chơi |
Dũng thắng |
Dũng thắng |
Nam thắng |
Dũng thắng |
Nam thắng |
Hòa |
Dũng thắng |
Dũng thắng |
Dũng thắng |
Nam thắng |
Trong 10 ván chơi, chỉ có 1 lần Dũng và Nam hòa nhau nên xác suất thực nghiệm của sự kiện “Dũng và Nam hòa nhau” là 
c) Nam không thua Dũng tức là Nam thắng Dũng hoặc Nam hòa Dũng.
Trong 10 ván chơi, có 3 lần Nam thắng và 1 lần hòa nhau nên xác suất thực nghiệm của sự kiện “Nam không thua Dũng” là 
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Trong 
số từ 
đến 
có 
số chia hết cho 
là 
Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 
là 
b) Trong số từ đến có 
số chia hết cho cả 
và là 
Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho cả và là 
c) Trong số từ đến có số có hai chữ số và tổng các chữ số bằng là 
Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng 
là
Lời giải
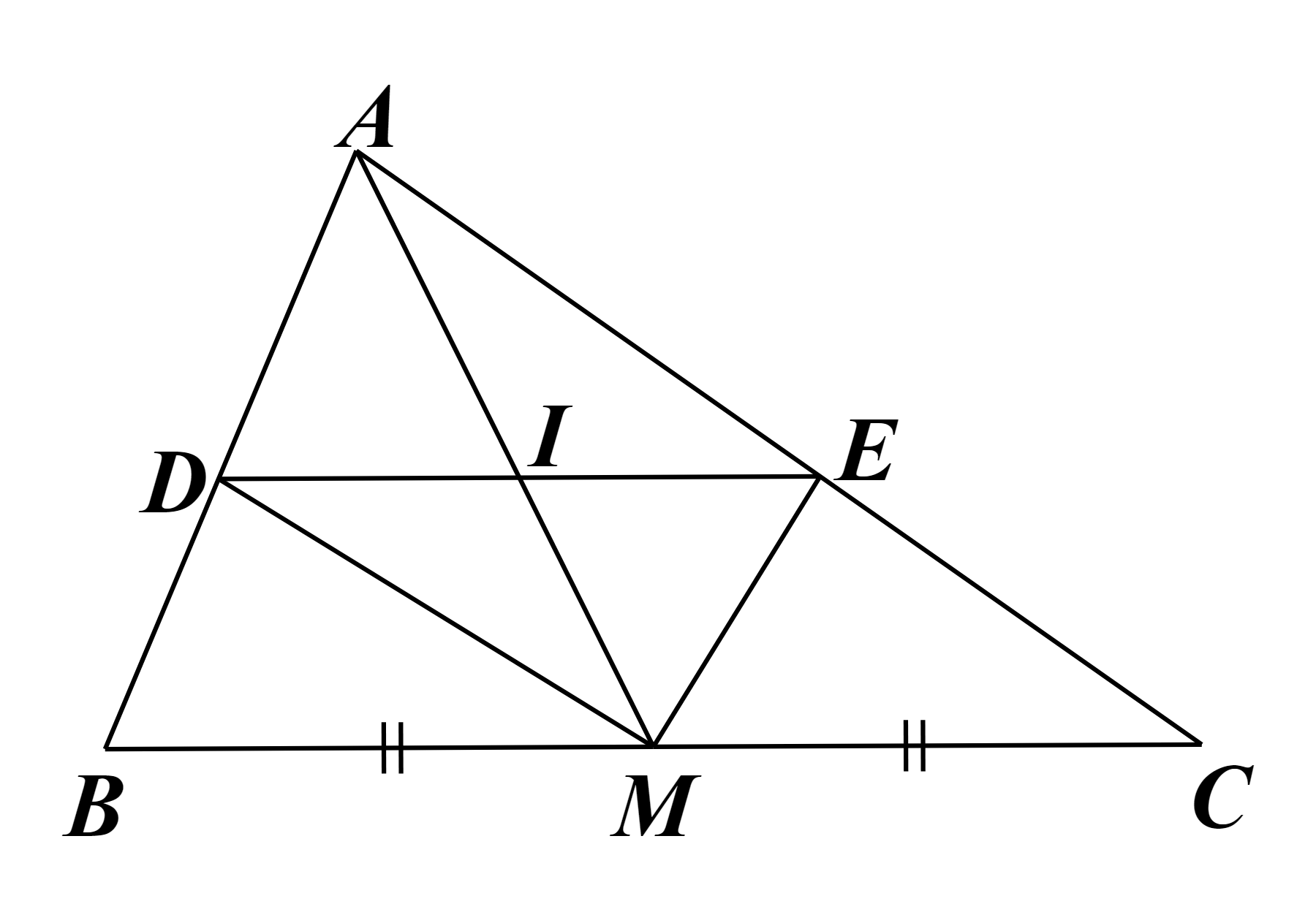
Xét 
có 
theo hệ quả định lí Thalès ta có 
Xét 
có 
theo hệ quả định lí Thalès ta có 
Do đó 
Mà 
(chứng minh ở câu a) nên 
hay 
là trung điểm của 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập