Cho 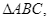 trung tuyến
trung tuyến 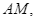 đường phân giác của
đường phân giác của 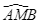 cắt
cắt 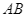 ở
ở 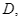 đường phân giác của
đường phân giác của 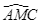 cắt
cắt 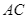 ở
ở 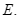 Gọi
Gọi  là giao điểm của
là giao điểm của 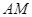 và
và 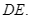 Tam giác
Tam giác 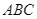 phải thêm điều kiện gì để
phải thêm điều kiện gì để 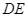 là đường trung bình của tam giác đó?
là đường trung bình của tam giác đó?
Quảng cáo
Trả lời:
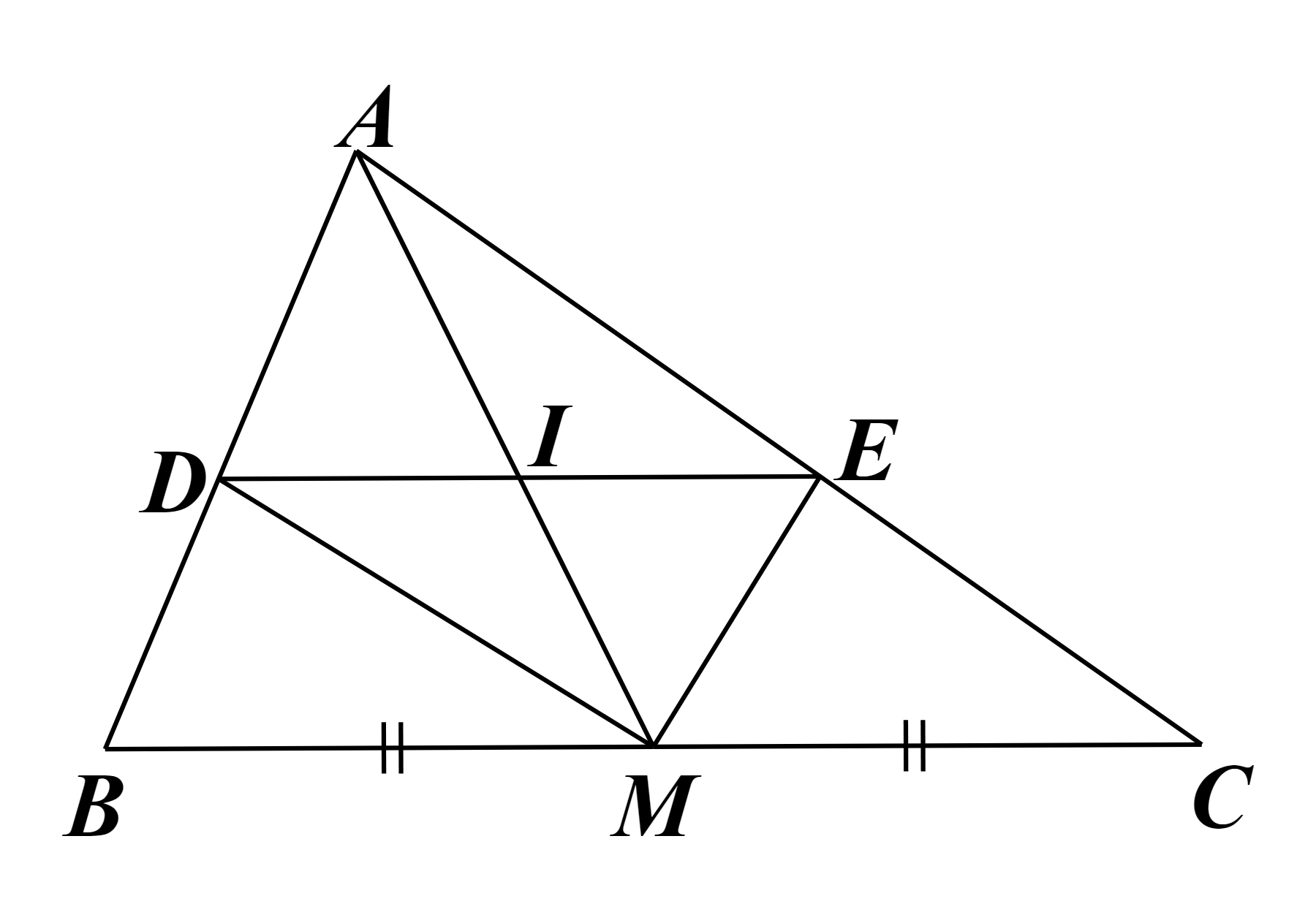
Để ![]() là đường trung bình của
là đường trung bình của ![]() thì
thì ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]()
Xét ![]() có
có ![]() vừa là đường trung tuyến, vừa là đường phân giác nên là tam giác cân tại
vừa là đường trung tuyến, vừa là đường phân giác nên là tam giác cân tại ![]() Suy ra
Suy ra ![]() (tính chất tam giác cân).
(tính chất tam giác cân).
Tương tự, ta cũng chứng minh được ![]()
Do đó ![]()
Xét ![]() có đường trung tuyến
có đường trung tuyến ![]() bằng nửa cạnh
bằng nửa cạnh ![]() nên
nên ![]() vuông tại
vuông tại ![]()
Vậy ![]() phải là tam giác vuông tại
phải là tam giác vuông tại ![]() thì
thì ![]() là đường trung bình của tam giác đó.
là đường trung bình của tam giác đó.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
b) Ta có bảng thống kê sau:
|
Lần thứ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Dũng |
L |
B |
B |
K |
L |
B |
K |
B |
K |
K |
|
Nam |
B |
K |
L |
L |
K |
B |
L |
K |
L |
B |
|
Kết quả ván chơi |
Dũng thắng |
Dũng thắng |
Nam thắng |
Dũng thắng |
Nam thắng |
Hòa |
Dũng thắng |
Dũng thắng |
Dũng thắng |
Nam thắng |
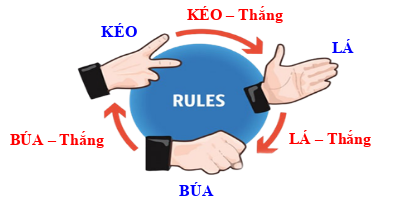
Trong 10 ván chơi, chỉ có 1 lần Dũng và Nam hòa nhau nên xác suất thực nghiệm của sự kiện “Dũng và Nam hòa nhau” là ![]()
c) Nam không thua Dũng tức là Nam thắng Dũng hoặc Nam hòa Dũng.
Trong 10 ván chơi, có 3 lần Nam thắng và 1 lần hòa nhau nên xác suất thực nghiệm của sự kiện “Nam không thua Dũng” là ![]()
Lời giải
a) Trong ![]() số từ
số từ ![]() đến
đến ![]() có
có ![]() số chia hết cho
số chia hết cho ![]() là
là ![]()
Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho ![]() là
là ![]()
b) Trong ![]() số từ
số từ ![]() đến
đến ![]() có
có ![]() số chia hết cho cả
số chia hết cho cả ![]() và
và ![]() là
là ![]()
Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho cả ![]() và
và ![]() là
là ![]()
c) Trong ![]() số từ
số từ ![]() đến
đến ![]() có
có ![]() số có hai chữ số và tổng các chữ số bằng
số có hai chữ số và tổng các chữ số bằng ![]() là
là ![]()
Xác suất của biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ số và tổng các chữ số bằng ![]() là
là ![]()
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.