Cho đường tròn tâm ![]() nội tiếp tam giác
nội tiếp tam giác ![]() tiếp xúc với
tiếp xúc với ![]() lần lượt tại
lần lượt tại ![]() và
và ![]() Kẻ
Kẻ ![]() vuông góc với
vuông góc với ![]() Chứng minh rằng:
Chứng minh rằng:
Tứ giác ![]() là tứ giác nội tiếp.
là tứ giác nội tiếp.
Quảng cáo
Trả lời:
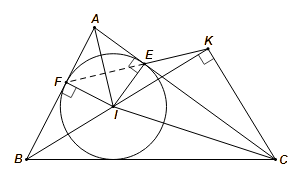
Vì ![]() là tiếp điểm của đường tròn
là tiếp điểm của đường tròn ![]() nội tiếp tam giác
nội tiếp tam giác ![]() nên
nên ![]()
Do đó ![]() , nên hai tam giác
, nên hai tam giác ![]() là hai tam giác vuông có cùng cạnh huyền
là hai tam giác vuông có cùng cạnh huyền ![]()
Do đó đường tròn ngoại tiếp hai tam giác ![]() là đường tròn đường kính
là đường tròn đường kính ![]() hay bốn điểm
hay bốn điểm ![]() cùng nằm trên đường tròn đường kính
cùng nằm trên đường tròn đường kính ![]()
Vậy tứ giác ![]() là tứ giác nội tiếp.
là tứ giác nội tiếp.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
Giả sử ba bông hoa màu đỏ là Đ1, Đ2, Đ3.
Không gian mẫu là ![]() {(Đ1, Vàng); (Đ2, Vàng); (Đ3, Vàng); (Đ1, Đ2); (Đ1, Đ3); (Đ2, Đ3)}.
{(Đ1, Vàng); (Đ2, Vàng); (Đ3, Vàng); (Đ1, Đ2); (Đ1, Đ3); (Đ2, Đ3)}.
Không gian mẫu có 6 phần tử.
Có 3 kết quả thuận lợi cho biến cố đã cho là: (Đ1, Vàng); (Đ2, Vàng); (Đ3, Vàng).
Vậy xác suất của biến cố đó là: ![]()
Lời giải
Đáp án đúng là: A
Kết quả của phép thử là ![]() trong đó
trong đó ![]() lần lượt là số chấm xuất hiện trên con xúc xắc thứ nhất và thứ hai.
lần lượt là số chấm xuất hiện trên con xúc xắc thứ nhất và thứ hai.
Các kết quả thuận lợi cho biến cố “Số chấm xuất hiện ở mặt trên của hai con xúc xắc giống nhau” là:
![]()
Như vậy có 6 kết quả thuận lợi cho biến cố đã cho.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Lấy ngẫu nhiên 1 viên bi từ hộp chứa 3 viên bi với 3 màu khác nhau.
B. Lấy ngẫu nhiên 1 quyển sách từ thùng chứa 4 quyển sách có độ dày khác nhau.
C. Lấy ngẫu nhiên 1 quyển vở từ thùng chứa 10 quyển vở giống nhau.
D. Gieo 1 con xúc xắc 6 mặt cân đối và đồng chất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.