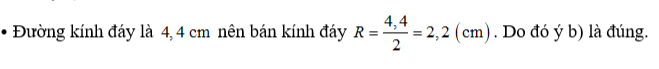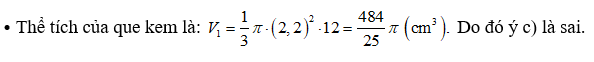Một chiếc kem ốc quế có dạng hình nón với phần vỏ quế có đường kính đáy là 4,4 cm chiều cao vỏ quế 12 cm. Người ta lấy phần kem từ một hộp hình trụ có chiều cao là 15 cm với diện tích đáy để cho vào vỏ ốc quế (coi phần vỏ kem có độ dày không đáng kể).
a) Thể tích hình trụ có bán kính đáy R và chiều cao h, được tính bằng công thức:
Một chiếc kem ốc quế có dạng hình nón với phần vỏ quế có đường kính đáy là 4,4 cm chiều cao vỏ quế 12 cm. Người ta lấy phần kem từ một hộp hình trụ có chiều cao là 15 cm với diện tích đáy để cho vào vỏ ốc quế (coi phần vỏ kem có độ dày không đáng kể).
Quảng cáo
Trả lời:
Sai

Câu hỏi cùng đoạn
Câu 4:
d) Ta có thể lấy kem từ hộp làm được tối đa 75 chiếc kem ốc quế.
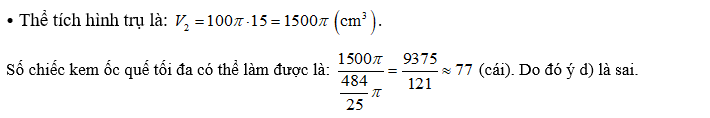
Câu 5:
d) Ta có thể lấy kem từ hộp làm được tối đa 75 chiếc kem ốc quế.
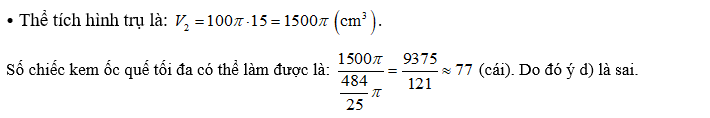
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
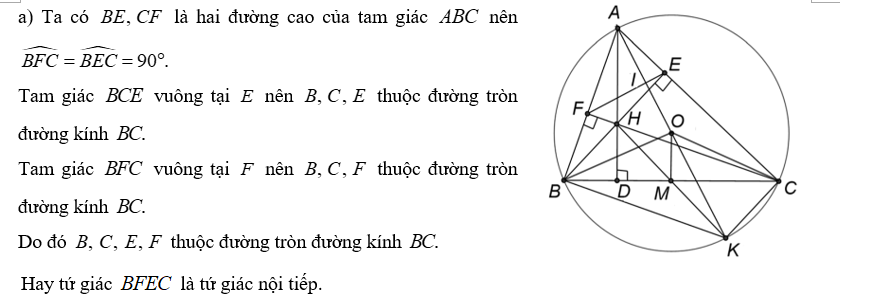
Bài 2. (1,5 điểm) Cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn (O;R). Các đường cao BE;CF của tam giác cắt nhau tại H (E thuộc AC , F thuộc AB).
a) Chứng minh: Tứ giác BFEC nội tiếp đường tròn.
b) Kẻ đường kính AK của đường tròn (O). Chứng minh AK vuông góc với È.
c) Giả sử BC cố định và A di chuyển trên cung lớn BC sao cho tam giác ABC luôn là tam giác nhọn. Xác định vị trí của điểm A để diện tích tam giác EAH lớn nhất. Tính giá trị lớn nhất đó theo R khi
Bài 2. (1,5 điểm) Cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn (O;R). Các đường cao BE;CF của tam giác cắt nhau tại H (E thuộc AC , F thuộc AB).
a) Chứng minh: Tứ giác BFEC nội tiếp đường tròn.
b) Kẻ đường kính AK của đường tròn (O). Chứng minh AK vuông góc với È.
c) Giả sử BC cố định và A di chuyển trên cung lớn BC sao cho tam giác ABC luôn là tam giác nhọn. Xác định vị trí của điểm A để diện tích tam giác EAH lớn nhất. Tính giá trị lớn nhất đó theo R khi
Lời giải


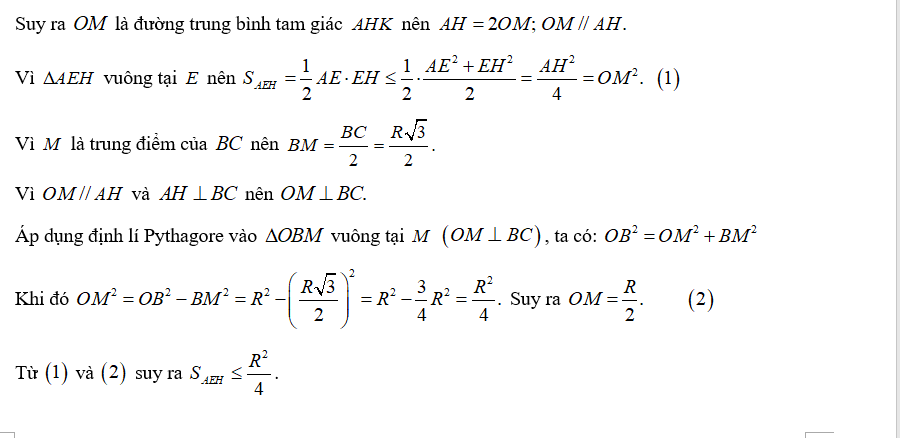
Lời giải
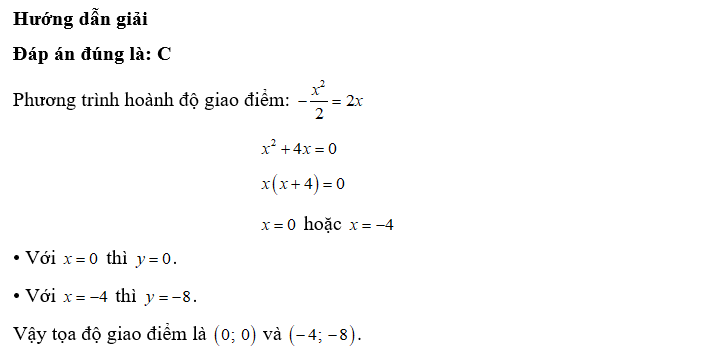
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.