Một hộp đựng 4 quả cầu xanh, 6 quả cầu đỏ, 5 quả cầu vàng, các quả cầu đều khác nhau. Chọn ngẫu nhiên 4 quả cầu từ hộp đó.
a) Số phần tử của không gian mẫu là 1356.
b) Xét biến cố \(A\): “Chọn được đúng 2 quả cầu xanh”. Khi đó \(n\left( A \right) = 330\).
c) Xác suất để chọn được 4 quả cầu có ít nhất 3 quả xanh là \(\frac{3}{{91}}\).
d) Xác suất để chọn được 4 quả cầu trong đó có ít nhất 1 quả đỏ là \(\frac{6}{{65}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) S, b) Đ, c) Đ, d) S
a) Ta có \(n\left( \Omega \right) = C_{15}^4 = 1365\).
b) Có \(n\left( A \right) = C_4^2.C_6^1.C_5^1 + C_4^2.C_6^2 + C_4^2.C_5^2 = 330\).
c) Số cách chọn được 4 quả cầu có ít nhất 3 quả xanh là \(C_4^3.C_6^1 + C_4^3.C_5^1 + C_4^4 = 45\).
Xác suất chọn được 4 quả cầu có ít nhất 3 quả xanh là \(\frac{{45}}{{1365}} = \frac{3}{{91}}\).
d) Số cách chọn 4 quả cầu không có quả màu đỏ là: \(C_4^1.C_5^3 + C_4^2.C_5^2 + C_4^3.C_5^1 = 90\).
Xác suất chọn được 4 quả cầu không có quả màu đỏ là \(\frac{{90}}{{1365}} = \frac{6}{{91}}\).
Suy ra xác suất để chọn được 4 quả cầu trong đó có ít nhất 1 quả đỏ là \(1 - \frac{6}{{91}} = \frac{{85}}{{91}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Chọn hệ trục tọa độ \(Oxy\) sao cho một chân cổng đặt tại gốc tọa độ, chân còn lại đặt trên tia \(Ox\). Khi đó cổng parabol là một phần của đồ thị hàm số dạng \(y = a{x^2} + bx\).
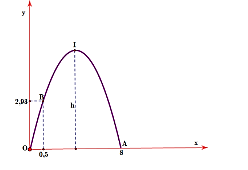
Vì parabol đi qua các điểm có tọa độ \(A\left( {8;0} \right)\) và \(B\left( {0,5;2,93} \right)\) nên ta có hệ
\(\left\{ \begin{array}{l}a{.8^2} + b.8 = 0\\a.0,{5^2} + b.0,5 = 2,93\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{{293}}{{375}}\\b = \frac{{2344}}{{375}}\end{array} \right.\). Suy ra \(\left( P \right):y = - \frac{{293}}{{375}}{x^2} + \frac{{2344}}{{375}}x\).
Hàm số có đỉnh \(I\left( {4;\frac{{4688}}{{375}}} \right)\). Suy ra chiều cao của cổng là \(\frac{{4688}}{{375}}\) m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Trả lời: 0,32
Gọi \(\Omega \) là không gian mẫu.
Có 9 cách lấy ra 1 viên bi từ hộp thứ nhất bỏ vào hộp thứ hai. Sau khi bỏ thì số viên bi trong hộp thứ hai là 13 viên. Khi đó có \(C_{13}^2\) cách lấy 2 viên bi từ hộp thứ hai.
Suy ra số phần tử không gian mẫu là \(n\left( \Omega \right) = 9C_{13}^2\).
Gọi \(A\) là biến cố: “Lấy được từ hộp thứ hai 2 viên bi trắng”.
TH1: Lấy được 1 viên bi xanh từ hộp thứ nhất bỏ vào hộp thứ hai.
Có 4 cách lấy ra một viên bi xanh từ hộp thứ nhất bỏ vào hộp thứ hai. Sau khi bỏ viên bi xanh lấy từ hộp thứ nhất vào hộp thứ hai thì số bi trắng trong hộp thứ hai vẫn là \(7\). Khi đó có \(C_7^2\) cách lấy hai viên bi trắng từ hộp thứ hai. Suy ra trong trường hợp này có \(4C_7^2\) cách.
TH2: Lấy được 1 viên bi trắng từ hộp thứ nhất bỏ vào hộp thứ hai.
Có 5 cách lấy ra một viên bi trắng từ hộp thứ nhất bỏ vào hộp thứ hai. Sau khi bỏ viên bi trắng lấy từ hộp thứ nhất vào hộp thứ hai thì số bi trắng trong hộp thứ hai là 8. Khi đó có \(C_8^2\) cách lấy 2 viên bi trắng từ hộp thứ hai. Suy ra trong trường hợp này có \(5C_8^2\) cách.
Suy ra \(n\left( A \right) = 4C_7^2 + 5C_8^2\) cách.
Do đó xác suất cần tính là \(P = \frac{{4C_7^2 + 5C_8^2}}{{9C_{13}^2}} = \frac{{112}}{{351}} \approx 0,32\).
Câu 3
A. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 5\).
B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 25\).
C. \({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\).
D. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 5\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(f\left( x \right) < 0,\forall x \in \mathbb{R}\).
</>
B. \(f\left( x \right) \ge 0,\forall x \in \mathbb{R}\).
C. \(f\left( x \right) \le 0,\forall x \in \mathbb{R}\).
D. \(f\left( x \right) > 0,\forall x \in \mathbb{R}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập