Trong hệ trục tọa độ \(Oxy\) cho hai điểm \(M\left( {4; - 3} \right),N\left( {4;1} \right)\) và đường thẳng \(d:x + 6y = 0\). Tìm bán kính (kết quả làm tròn đến hàng phần trăm) của đường tròn \(\left( C \right)\) đi qua \(M\) và \(N\) biết rằng các tiếp tuyến của \(\left( C \right)\) tại \(M\) và \(N\) cắt nhau tại điểm \(Q\) thuộc \(d\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Trả lời: 2,83
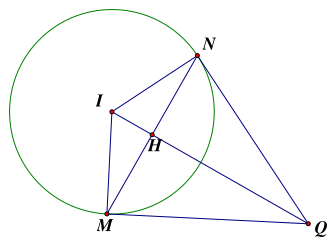
Gọi \(I\) là tâm của đường tròn \(\left( C \right)\), \(H\) là trung điểm của \(MN\).
Suy ra \(H\left( {4; - 1} \right)\), \(\overrightarrow {MN} = \left( {0;4} \right) = 4\left( {0;1} \right)\).
Đường thẳng \(IQ\) đi qua điểm \(H\left( {4; - 1} \right)\) và nhận \(\overrightarrow n \left( {0;1} \right)\) làm vectơ pháp tuyến có phương trình là:
\(y + 1 = 0\).
Tọa độ điểm \(Q\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 6y = 0\\y + 1 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 1\end{array} \right.\). Do đó \(Q\left( {6; - 1} \right)\).
Ta có \[\overrightarrow {MQ} = \left( {2;2} \right)\], \(\overrightarrow {NQ} = \left( {2; - 2} \right)\).
Đường thẳng \(IM\) đi qua \(M\left( {4; - 3} \right)\) và nhận \(\overrightarrow {MQ} \) làm vectơ pháp tuyến có phương trình là:
\(2\left( {x - 4} \right) + 2\left( {y + 3} \right) = 0\)\( \Leftrightarrow x + y - 1 = 0\).
Đường thẳng \(IN\) đi qua \(N\left( {4;1} \right)\) và nhận \(\overrightarrow {NQ} \) làm vectơ pháp tuyến có phương trình là:
\(2\left( {x - 4} \right) - 2\left( {y - 1} \right) = 0\)\( \Leftrightarrow x - y - 3 = 0\).
Tọa độ điểm \(I\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + y = 1\\x - y = 3\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = - 1\end{array} \right.\). Do đó \(I\left( {2; - 1} \right)\).
Bán kính của đường tròn \(\left( C \right)\) là \(R = IM = \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( { - 3 + 1} \right)}^2}} = 2\sqrt 2 \approx 2,83\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Không gian mẫu \(n\left( \Omega \right) = C_{18}^3 = 816\).
Gọi C là biến cố: “Chọn được nhiều nhất hai viên bi xanh”.
Th1: Chọn 2 bi xanh và 1 bi trong 6 bi đỏ và 7 bi vàng có \(C_5^2.C_{13}^1 = 130\) cách.
Th2: Chọn 1 bi xanh và 2 bi trong 6 bi đỏ và 7 bi vàng có \(C_5^1.C_{13}^2 = 390\) cách.
Th3: Chọn 0 bi xanh và 3 bi trong 6 bi đỏ và 7 bi vàng có \(C_{13}^3 = 286\) cách.
Suy ra \(n\left( C \right) = 130 + 390 + 286 = 806\).
Xác suất của biến cố \(C\) là \(P\left( C \right) = \frac{{806}}{{816}} = \frac{{403}}{{408}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Trả lời: 49
Hai thẻ lấy ra có tổng là một số chẵn khi 2 số đó cùng chẵn hoặc cùng lẻ.
Từ 1 đến 15 có 7 số chẵn và 8 số lẻ.
Số kết quả thuận lợi cho biến cố là \(C_7^2 + C_8^2 = 49\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Biến cố.
B. Xác suất.
C. Không gian mẫu của phép thử.
D. Phép thử.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(x = - 3\).
B. \(x = - 2\).
C. \(x = 1\).
D. \(x = 2\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập