Câu hỏi:
18/03/2025 72
(0,5 điểm) Giải phương trình \(2x{\left( {8x - 1} \right)^2}\left( {4x - 1} \right) = 9.\)
(0,5 điểm) Giải phương trình \(2x{\left( {8x - 1} \right)^2}\left( {4x - 1} \right) = 9.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(2x{\left( {8x - 1} \right)^2}\left( {4x - 1} \right) = 9\)
\(8x{\left( {8x - 1} \right)^2}\left( {8x - 2} \right) = 72\).
Đặt \(y = 8x - 1,\) ta được: \(\left( {y + 1} \right){y^2}\left( {y - 1} \right) = 72\)
\(\left( {{y^2} - 9} \right)\left( {{y^2} + 8} \right) = 0\)
\({y^2} - 9 = 0\) (vì \({y^2} + 8 > 0\))
Do đó, \({y^2} = 9\) nên \(y = 3\) hoặc \(y = - 3\).
• Với \(y = 3\) thì \(8x - 1 = 3\) nên \(8x = 4\), suy ra \(x = \frac{1}{2}.\)
• Với \(y = - 3\) thì \(8x - 1 = - 3\) nên \(8x = - 2\), suy ra \(x = - \frac{1}{4}.\)
Vậy nghiệm của phương trình là \(S = \left\{ {\frac{1}{2}; - \frac{1}{4}} \right\}.\)
Sách thầy cô Vietjack biên soạn
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
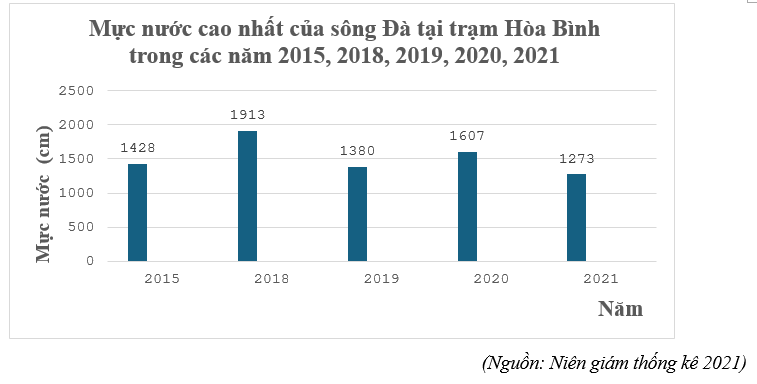
Biều đồ cột ở hình bên dưới thống kê mực nước cao nhất của sông Đà tại tạm Hòa Bình trong các năm 2015, 2018, 2019, 2020, 2021.
Hỏi năm 2021 mực nước cao nhất của sông Đà tại trạm Hoài Bình đã giảm bao nhiêu phần trăm so với năm 2019? (Kết quả làm tròn đến hàng phần trăm)
Xem đáp án »
18/03/2025
603
Câu 7:
Tìm giá trị của \(x\), biết: \(4\left( {0,5 - 1,5x} \right) = - \frac{{5x - 6}}{3}.\)
Tìm giá trị của \(x\), biết: \(4\left( {0,5 - 1,5x} \right) = - \frac{{5x - 6}}{3}.\)
Xem đáp án »
18/03/2025
143
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
-
Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận