Quảng cáo
Trả lời:
Ta có: \[A = ab{\left( {b - {\rm{ }}a} \right)^2} = \frac{1}{4} \cdot 4ab\left( {{a^2} - 2ab + {b^2}} \right)\]
\[ \le \frac{1}{4} \cdot \frac{1}{4}{\left( {4ab + {a^2} - 2ab + {b^2}} \right)^2}\]
\[ = \frac{1}{{16}}{\left( {{a^2} + 2ab + {b^2}} \right)^2}\]
\[ = \frac{1}{{16}}{\left( {a + b} \right)^4} = \frac{1}{{16}} \cdot {1^4} = \frac{1}{{16}}.\]
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}4ab = {a^2}--2ab + {b^2}\\a + b = 1\end{array} \right.\)hay \(\left\{ \begin{array}{l}a = \frac{{2 + \sqrt 2 }}{4}\\b = \frac{{2 - \sqrt 2 }}{4}\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}a = \frac{{2 - \sqrt 2 }}{4}\\b = \frac{{2 + \sqrt 2 }}{4}\end{array} \right.\)
Vậy giá trị lớn nhất của biểu thức A bằng \(\frac{1}{{16}}\) khi \(\left( {a;b} \right) \in \left\{ {\left( {\frac{{2 + \sqrt 2 }}{4};\,\,\frac{{2 - \sqrt 2 }}{4}} \right);\,\,\left( {\frac{{2 - \sqrt 2 }}{4};\,\,\frac{{2 + \sqrt 2 }}{4}} \right)} \right\}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Có các dấu hiệu nhận biết một số bất kỳ có chia hết cho gồm:
• Để nhận biết một số có thể chia hết cho 7, ta cắt giảm chữ số cuối cùng đi 1 số, nhân đôi số đó và lấy số cắt giảm trừ đi số đã nhân đôi. Điều này cần được thực hiện lặp đi lặp lại một vài lần, đến khi thu được một số có thể chia hết cho 7 thì số đã cho chia hết cho 7.
Ví dụ: Số 3 101 có chia hết cho 7 hay không?
Các bước thực hiện:
− Giảm chữ số cuối cùng của số 3 101 đi chữ số 1 còn 310
− Nhân đôi chữ số cắt giảm (2 . 1 = 2) và lấy số còn lại sau cắt giảm trừ đi nó:
310 – 2 = 308
− Lặp lại quy trình bằng cách giảm đi 8 của 308 còn 30
− Nhân đôi số 8 cho (2 . 8 = 16) và trừ đi số đó: 30 – 16 = 14
− Nhận được Số là 14 là số chia hết cho 7
Kết luận: Số 3 101 chia hết cho 7
• Lấy chữ số đầu tiên nhân với 3 rồi cộng thêm chữ số tiếp theo, được bao nhiêu lại nhân với 3 rồi cộng thêm chữ số tiếp theo… cứ như vậy cho đến chữ số cuối cùng của số cần nhận biết. Nếu kết quả cuối cùng này chia hết cho 7 thì số đó chia hết cho 7.
Ví dụ: Số cần nhận biết là 203:
Lấy 2 . 3 = 6 rồi lấy 6 + 0 = 6 tiếp theo lấy 3 . 6 = 18 sau đó 18 + 3 = 21.
Do đó 203 chia hết cho 7.
Lời giải
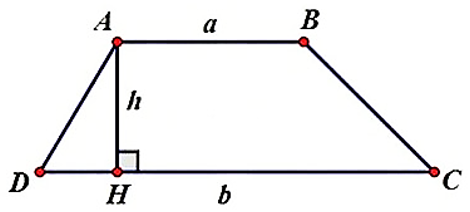
Công thức tính đáy lớn b khi biết diện tích S và đáy lớn a:
b = \(\frac{{2S}}{h} - a\)
Trong đó:
b là độ dài đáy lớn
S: Diện tích của hình thang
a: Độ dài đáy bé
h : Chiều cao
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.