Cho bất phương trình 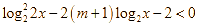 . Số giá trị nguyên của tham số
. Số giá trị nguyên của tham số 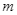 thuộc đoạn
thuộc đoạn 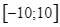 để bất phương trình đã cho có nghiệm thuộc khoảng
để bất phương trình đã cho có nghiệm thuộc khoảng 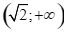 là:
là:
Cho bất phương trình 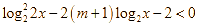 . Số giá trị nguyên của tham số
. Số giá trị nguyên của tham số ![]() thuộc đoạn
thuộc đoạn ![]() để bất phương trình đã cho có nghiệm thuộc khoảng
để bất phương trình đã cho có nghiệm thuộc khoảng ![]() là:
là:
Quảng cáo
Trả lời:
Đáp án đúng là A
Phương pháp giải
Đặt ẩn phụ rồi đưa bất phương trình đã cho về bất phương trình bậc hai.
Lời giải
Điều kiện: ![]() .
.
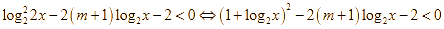 (1)
(1)Đặt ![]() . Vì
. Vì ![]() nên
nên ![]() . Khi đó (1) trở thành:
. Khi đó (1) trở thành: 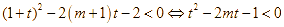 (2).
(2).
Yêu cầu bài toán trở thành: tìm ![]() để (2) có nghiệm thuộc
để (2) có nghiệm thuộc ![]() . Mà
. Mà ![]() có
có ![]() và
và ![]() nên
nên ![]() luôn có hai nghiệm phân biệt
luôn có hai nghiệm phân biệt ![]()
Do đó, để (2) có nghiệm thuộc ![]() thì:
thì: ![]()
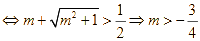 .
.
Mà ![]() là số nguyên thuộc đoạn
là số nguyên thuộc đoạn ![]() nên có 11 giá trị của
nên có 11 giá trị của ![]() thỏa yêu cầu bài toán.
thỏa yêu cầu bài toán.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là A
Phương pháp giải
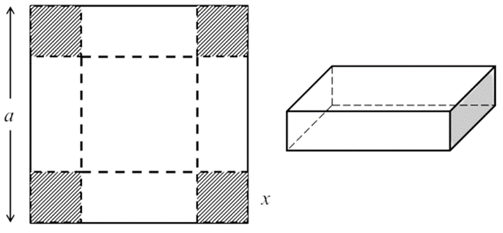
Lập hàm số thể tích cái hộp không nắp theo biến ![]() , sau đó tìm giá trị lớn nhất của hàm số vừa lập.
, sau đó tìm giá trị lớn nhất của hàm số vừa lập.
Lời giải
Cạnh đáy của cái hộp không nắp là ![]() . Điều kiện:
. Điều kiện: ![]() .
.
Thể tích của cái hộp không nắp là ![]()
Xét hàm số ![]() trên
trên ![]()
![]() liên tục trên
liên tục trên ![]()
![]()
![]() (loại)
(loại)
BBT
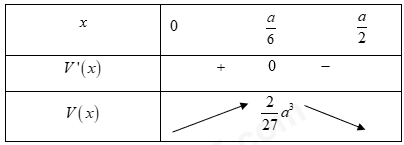
Dựa vào 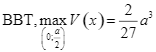 đạt tại
đạt tại ![]() . Khi đó, cạnh đáy của cái hộp là
. Khi đó, cạnh đáy của cái hộp là ![]() .
.
Lời giải
Đáp án đúng là B
Phương pháp giải
Công thức Bayes: 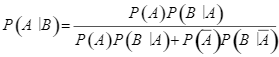 .
.
Lời giải
Gọi ![]() là biến cố "người được chọn nghiện thuốc lá".
là biến cố "người được chọn nghiện thuốc lá".
Gọi ![]() là biến cố "người được chọn bị bệnh phổi".
là biến cố "người được chọn bị bệnh phổi".
Ta cần tính ![]() .
.
Ta có: ![]() .
.
Theo công thức Bayes, ta có
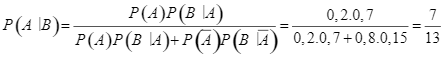
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. tháng 2 năm 2023.
C. tháng 4 năm 2023.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. tồn tại dưới dạng cation và di chuyển về cực âm (−) nguồn điện.
B. tồn tại dưới dạng anion và di chuyển về cực dương (+) nguồn điện.
C. tồn tại dưới dạng anion và di chuyển về cực âm (−) nguồn điện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 0,31(s)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.