Một bài thi nọ gồm 50 câu hỏi theo hình thức trắc nghiệm khách quan, mỗi câu có 4 phương án lựa chọn. Ứng với mỗi câu hỏi, thí sinh chỉ được chọn duy nhất một phương án mà mình cho là đúng. Nếu chọn đúng đáp án, thí sinh sẽ được cộng 0,2 điểm, còn nếu chọn sai, thí sinh sẽ không được cộng điểm nào.
Sau khi đọc hiểu xong câu hỏi thứ nhất và thứ hai của bài thi, bạn Sơn biết mình không thể làm được nên quyết định chọn phương án một cách ngẫu nhiên cho cả hai câu. Xác suất để Sơn trả lời đúng cho cả hai câu này là:
Một bài thi nọ gồm 50 câu hỏi theo hình thức trắc nghiệm khách quan, mỗi câu có 4 phương án lựa chọn. Ứng với mỗi câu hỏi, thí sinh chỉ được chọn duy nhất một phương án mà mình cho là đúng. Nếu chọn đúng đáp án, thí sinh sẽ được cộng 0,2 điểm, còn nếu chọn sai, thí sinh sẽ không được cộng điểm nào.
Sau khi đọc hiểu xong câu hỏi thứ nhất và thứ hai của bài thi, bạn Sơn biết mình không thể làm được nên quyết định chọn phương án một cách ngẫu nhiên cho cả hai câu. Xác suất để Sơn trả lời đúng cho cả hai câu này là:
Quảng cáo
Trả lời:
Đáp án đúng là D
Phương pháp giải
Cho ![]() và
và ![]() là hai biến cố độc lập. Xác suất để biến cố
là hai biến cố độc lập. Xác suất để biến cố ![]() và
và ![]() cùng xảy ra là
cùng xảy ra là![]() .
.
Lời giải
Gọi ![]() là biến cố "chọn đúng đáp án câu thứ nhất".
là biến cố "chọn đúng đáp án câu thứ nhất".
Gọi ![]() là biến cố "chọn đúng đáp án câu thứ hai".
là biến cố "chọn đúng đáp án câu thứ hai".
Ta có: ![]() . Do
. Do ![]() là các biến cố độc lập nên xác suất để chọn đúng đáp án cả hai câu là:
là các biến cố độc lập nên xác suất để chọn đúng đáp án cả hai câu là: ![]() .
.
Câu hỏi cùng đoạn
Câu 2:
Bạn Thủy - một trong những thí sinh xuất sắc của kì thi lần này - chắc chắn làm đúng 47 câu hỏi, số còn lại vì sắp hết giờ nên Thủy quyết định chọn phương án một cách ngẫu nhiên. Xác suất để Thủy đạt được điểm số không dưới 9,8 là
Bạn Thủy - một trong những thí sinh xuất sắc của kì thi lần này - chắc chắn làm đúng 47 câu hỏi, số còn lại vì sắp hết giờ nên Thủy quyết định chọn phương án một cách ngẫu nhiên. Xác suất để Thủy đạt được điểm số không dưới 9,8 là
Đáp án đúng là C
Phương pháp giải
Cho ![]() và
và ![]() là hai biến cố độc lập. Khi đó,
là hai biến cố độc lập. Khi đó, ![]() và
và ![]() và
và ![]() và
và ![]() cũng độc lập.
cũng độc lập.
Do đó: ![]() ;
; ![]() .
.
Lời giải
Số câu hỏi Thủy chọn phương án một cách ngẫu nhiên là 3 câu.
Thủy đạt được điểm số không dưới 9,8 khi và chỉ khi trong 3 câu chọn phương án một cách ngẫu nhiên, Thủy trả lời đúng ít nhất 2 câu.
Xác suất để Thủy trả lời đúng cả 3 câu nêu trên là ![]()
Xác suất để Thủy trả lời đúng 2 trong số 3 câu nêu trên là ![]()
Vậy xác suất để Thủy đạt được điểm số không dưới 9,8 là ![]() .
.
Câu 3:
Bạn Cường không ôn bài nên đã chọn phương án ngẫu nhiên ở tất cả các câu hỏi. Xác suất để Cường đạt điểm 4 gần nhất với số nào dưới đây?
Bạn Cường không ôn bài nên đã chọn phương án ngẫu nhiên ở tất cả các câu hỏi. Xác suất để Cường đạt điểm 4 gần nhất với số nào dưới đây?
Đáp án đúng là B
Phương pháp giải
Sử dụng công thức Bernoulli để tính xác suất trong ![]() phép thử độc lập, biến cố
phép thử độc lập, biến cố ![]() xảy ra
xảy ra ![]() lần (mỗi lần có
lần (mỗi lần có ![]() như nhau) là:
như nhau) là: ![]()
Lời giải
Để Cường đạt điểm 4 thì Cường cần trả lời đúng 20 câu, trả lời sai 30 câu.
Vì Cường chọn phương án ngẫu nhiên ở tất cả các câu nên xác suất trả lời đúng mỗi câu của Cường là ![]() , xác suất trả lời sai mỗi câu của Cường là
, xác suất trả lời sai mỗi câu của Cường là ![]() .
.
Xác suất để Cường đạt điểm 4 là ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là A
Phương pháp giải
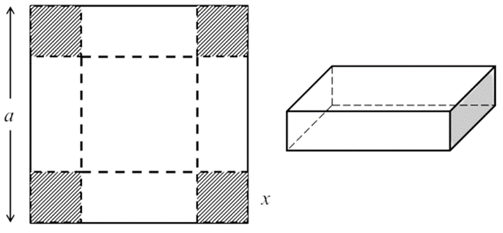
Lập hàm số thể tích cái hộp không nắp theo biến ![]() , sau đó tìm giá trị lớn nhất của hàm số vừa lập.
, sau đó tìm giá trị lớn nhất của hàm số vừa lập.
Lời giải
Cạnh đáy của cái hộp không nắp là ![]() . Điều kiện:
. Điều kiện: ![]() .
.
Thể tích của cái hộp không nắp là ![]()
Xét hàm số ![]() trên
trên ![]()
![]() liên tục trên
liên tục trên ![]()
![]()
![]() (loại)
(loại)
BBT
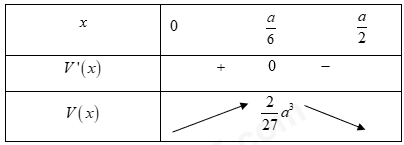
Dựa vào 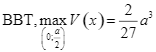 đạt tại
đạt tại ![]() . Khi đó, cạnh đáy của cái hộp là
. Khi đó, cạnh đáy của cái hộp là ![]() .
.
Lời giải
Đáp án đúng là B
Phương pháp giải
Công thức Bayes: 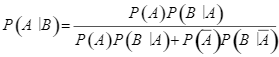 .
.
Lời giải
Gọi ![]() là biến cố "người được chọn nghiện thuốc lá".
là biến cố "người được chọn nghiện thuốc lá".
Gọi ![]() là biến cố "người được chọn bị bệnh phổi".
là biến cố "người được chọn bị bệnh phổi".
Ta cần tính ![]() .
.
Ta có: ![]() .
.
Theo công thức Bayes, ta có
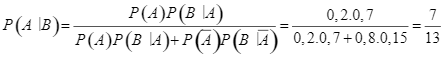
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. tháng 2 năm 2023.
C. tháng 4 năm 2023.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. tồn tại dưới dạng cation và di chuyển về cực âm (−) nguồn điện.
B. tồn tại dưới dạng anion và di chuyển về cực dương (+) nguồn điện.
C. tồn tại dưới dạng anion và di chuyển về cực âm (−) nguồn điện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 0,31(s)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.